2021-2022學年河南省鄭州市高二（上）期末數學試卷（理科）

一、選擇題：本大題共12個小題，每小題5分，共60分．在每小題所給出的四個選項中，只有一項是符合題目要求的．

• 1．命題：“?x＞1，x²≥1”的否定是（　　）

  A．?x＞1，x2＜1	B．?x0≤1，x02＜1
  C．?x0≤1，x02≥1	D．?x0＞1，x02＜1
  組卷：24引用：2難度：0.9

  解析

• 2．已知

  a

  =（1，2，y），

  b

  =（x,1，2），且

  a

  ∥

  b

  ，則x?y=（　　）

  A．1

  B．-1

  C．-2

  D．2
  組卷：136引用：4難度：0.8

  解析

• 3．△ABC中，三邊長之比為7：15：20，則△ABC為（　　）

  A．銳角三角形	B．直角三角形
  C．鈍角三角形	D．不存在這樣的三角形
  組卷：63引用：2難度：0.7

  解析

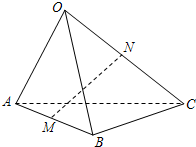• 4．已知三棱錐O-ABC，點M，N分別為AB，OC的中點，且

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，用

  a

  ，

  b

  ，

  c

  表示

  MN

  ，則

  MN

  等于（　　）

  A． 1 2 （ b + c - a ）

  B． 1 2 （ a + b - c ）

  C． 1 2 （ a - b + c ）

  D． 1 2 （ c - a - b ）
  組卷：2965引用：41難度：0.9

  解析

• 5．在△ABC中，a=x,

  b

  =

  3

  ，

  A

  =

  π

  3

  ，若該三角形有兩個解，則x范圍是（　　）

  A． （ 3 ， 6 ）

  B． （ 2 ， 2 3 ）

  C． [ 3 2 ， 3 ）

  D． （ 3 2 ， 3 ）
  組卷：529引用：4難度：0.8

  解析

• 6．等差數列{a_n}中，a₂+a₁₁+a₁₄=9，則前17項的和a₁+a₂+a₃+?+a₁₇=（　　）

  A．0

  B．17

  C．34

  D．51
  組卷：127引用：2難度：0.8

  解析

• 7．甲、乙兩名同學同時從教室出發去體育館打球（路程相等），甲一半時間步行，一半時間跑步；乙一半路程步行，一半路程跑步．如果兩人步行速度、跑步速度均相等，則（　　）

  A．甲先到體育館	B．乙先到體育館
  C．兩人同時到體育館	D．不確定誰先到體育館
  組卷：22引用：1難度：0.6

  解析

三、解答題：本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

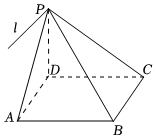• 21．如圖，四棱錐P-ABCD的底面為正方形，PD⊥底面ABCD，設平面PAD與平面PBC的交線為l.
  （Ⅰ）證明：l∥AD；
  （Ⅱ）已知PD=AD=1，Q為直線l上的點，求PB與平面QCD所成角的正弦值的最大值．
  組卷：191引用：2難度：0.4

  解析

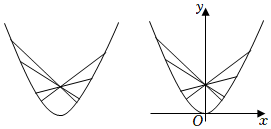• 22．在水平桌面上放一只內壁光滑的玻璃水杯，已知水杯內壁為拋物面型（拋物面指拋物線繞其對稱軸旋轉180°所得到的面），拋物面的軸截面是如圖所示的拋物線．現有一些長短不一、質地均勻的細直金屬棒，其長度均不小于拋物線通徑的長度（通徑是過拋物線焦點，且與拋物線的對稱軸垂直的直線被拋物線截得的弦），若將這些細直金屬棒，隨意丟入該水杯中，實驗發現：當細棒重心最低時，達到靜止狀態，此時細棒交匯于一點．
  （Ⅰ）請結合你學過的數學知識，猜想細棒交匯點的位置；
  （Ⅱ）以玻璃水杯內壁軸截面的拋物線頂點為原點，建立如圖所示直角坐標系．設玻璃水杯內壁軸截面的拋物線方程為x²=2py,將細直金屬棒視為拋物線的弦AB，且弦AB長度為a（a≥2p），以細直金屬棒的中點為其重心，請從數學角度解釋上述實驗現象．
  組卷：35引用：1難度：0.5

  解析