2022-2023學(xué)年山東省淄博五中高一（下）分班數(shù)學(xué)試卷（3月份）

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．集合A={-3，-2，-1，0，1，2}，集合

  B

  =

  {

  x

  |

  -

  1

  2

  ＜

  x

  ＜

  3

  2

  }

  ，則A∩B=（　　）

  A．{-1，0，1}

  B．{0，1}

  C．{0，1，2}

  D．?
  組卷：17引用：2難度：0.8

  解析

• 2．命題：“?x∈R，sinx≤1”的否定是（　　）

  A．?x∈R，sinx＞1	B．?x∈R，sinx≤1
  C．?x∈R，sinx＞1	D．?x∈R，sinx≥1
  組卷：135引用：11難度：0.9

  解析

• 3．設(shè)tanα=3，則

  sin

  （

  α

  -

  π

  ）

  +

  cos

  （

  π

  -

  α

  ）

  sin

  （

  π

  2

  -

  α

  ）

  +

  cos

  （

  π

  2

  +

  α

  ）

  =（　　）

  A．3

  B．2

  C．1

  D．-1
  組卷：1244引用：21難度：0.9

  解析

• 4．已知扇形OAB的面積為2，弧長(zhǎng)

  ?

  AB

  =

  2

  ，則AB=（　　）

  A．2sin1

  B． 2 sin 1 2

  C．4sin1

  D． 4 sin 1 2
  組卷：256引用：4難度：0.7

  解析

• 5．若a=e^0.5，b=sin

  22

  π

  5

  ，

  c

  =

  lo

  g

  2

  0.2，則a、b、c的大小關(guān)系為（　　）

  A．b＞a＞c

  B．a(chǎn)＞b＞c

  C．c＞a＞b

  D．b＞c＞a
  組卷：209引用：9難度：0.9

  解析

• 6．我國(guó)著名數(shù)學(xué)家華羅庚先生曾說：“數(shù)缺形時(shí)少直觀，形少數(shù)時(shí)難入微，數(shù)形結(jié)合百般好，隔離分家萬事休．”在數(shù)學(xué)的學(xué)習(xí)和研究中，常用函數(shù)圖象來研究函數(shù)性質(zhì)，也常用函數(shù)解析式來分析函數(shù)圖象的特征．如函數(shù)y=2^|x|sin2x的圖象大致是（　　）

  A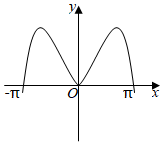．	B．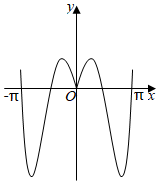
  C．	D．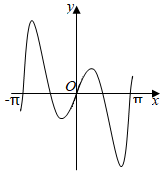
  組卷：149引用：5難度：0.9

  解析

• 7．基本再生數(shù)R₀與世代間隔T是流行病學(xué)基本參數(shù)，基本再生數(shù)是指一個(gè)感染者傳染的平均人數(shù)，世代間隔指兩代間傳染所需的平均時(shí)間，在α型病毒疫情初始階段，可以用指數(shù)模型I（t）=e^rt描述累計(jì)感染病例數(shù)I（t）隨時(shí)間t（（單位：天）的變化規(guī)律，指數(shù)增長(zhǎng)率r與R₀、T近似滿足R₀=1+rT，有學(xué)者基于已有數(shù)據(jù)估計(jì)出R₀=3.22，T=10．據(jù)此，在α型病毒疫情初始階段，累計(jì)感染病例數(shù)增加至I（0）的3倍需要的時(shí)間約為（　　）（參考數(shù)據(jù)：ln3≈1.10）

  A．2天

  B．3天

  C．4天

  D．5天
  組卷：184引用：4難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

• 21．已知角α的頂點(diǎn)與原點(diǎn)重合，始邊與x軸正半軸重合，終邊在直線y=2x上．則：
  （1）求

  cos

  （

  2

  α

  +

  π

  4

  ）

  的值；
  （2）已知

  α

  ∈

  （

  0

  ，

  π

  2

  ）

  ，

  sin

  （

  β

  +

  π

  4

  ）

  =

  10

  10

  ，-

  π

  2

  ＜

  β

  ＜

  0

  ，求α-β的值．
  組卷：180引用：3難度：0.6

  解析

• 22．已知函數(shù)f（x）=

  m

  x

  2

  -

  mx

  +

  2

  ．
  （1）若f（x）的定義域?yàn)镽，求實(shí)數(shù)m的取值范圍；
  （2）設(shè)函數(shù)g（x）=f（x）-

  2

  x,若g（lnx）≤0對(duì)任意的x∈[e,e²]恒成立，求實(shí)數(shù)m的取值范圍．
  組卷：158引用：2難度：0.5

  解析