當前位置：試卷中心 > 試卷詳情

2022-2023學年天津市濱海新區塘沽一中高二（上）期末數學試卷

發布：2024/4/20 14:35:0

一、選擇題（共12小題，每小題5分，滿分60分）

1．若直線過點（1，2），（4，2+
3
），則此直線的傾斜角是（　　）
A．30° B．45° C．60° D．90°
組卷：584引用：25難度：0.9
解析
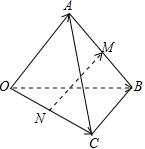2．三棱錐O-ABC中，M，N分別是AB，OC的中點，且
OA
=
a
，
OB
=
b
，
OC
=
c
，用
a
，
b
，
c
表示
NM
，則
NM
等于（　　）
A．
1
2
（-
a
+
b
+
c
） B．
1
2
（
a
+
b
-
c
） C．
1
2
（
a
-
b
+
c
） D．
1
2
（-
a
-
b
+
c
）
組卷：2295引用：19難度：0.9
解析
3．設平面β的一個法向量為
m
=
（
2
，-
1
，
z
）
，平面α的一個法向量為
n
=
（
4
，-
2
，-
2
）
，若平面β⊥平面α，則實數z的值為（　　）
A．3 B．4 C．5 D．6
組卷：199引用：2難度：0.8
解析
4．已知等差數列{a_n}的前n項和為S_n，且S₂₁=21，則a₆+a₁₆的值為（　　）
A．1 B．2 C．3 D．4
組卷：813引用：4難度：0.8
解析
5．下列求導運算正確的是（　　）
A．（lnx）′=x B．
（
sin
π
5
）
′
=
cos
π
5
C．（cosx）′=sinx D．（a^x）′=a^xlna（a＞0，a≠1）
組卷：582引用：2難度：0.7
解析
6．如圖，在直三棱柱ABC-A₁B₁C₁中，已知AB⊥AC，D為CC₁的中點，AB=AC=AA₁，則AB₁，A₁D所成角的余弦值是（　　）
A．
5
5
B．
3
6
C．
10
10
D．
10
20
組卷：191引用：3難度：0.6
解析
7．已知F₁，F₂是橢圓E：
x
2
8
+
y
2
12
=1的兩個焦點，過點F₁且斜率為k的直線l與E交于M，N兩點，則△MNF₂的周長為（　　）
A．8 B．8
2
C．8
3
D．與k有關
組卷：475引用：4難度：0.7
解析
8．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線方程為y=
2
5
5
x,且與橢圓
x
2
15
+
y
2
6
=1有公共焦點，則C的方程為（　　）
A．
x
2
8
-
y
2
10
=
1
B．
x
2
4
-
y
2
5
=
1
C．
x
2
5
-
y
2
4
=
1
D．
x
2
4
-
y
2
3
=
1
組卷：626引用：8難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共4小題，滿分50分）

23．已知正項等差數列{a_n}與等比數列{b_n}滿足a₁=1，b₂=4，且a₂既是a₁+b₁和b₃-a₃的等差中項，又是其等比中項．
（1）求數列{a_n}和{b_n}的通項公式．
（2）求數列
{
1
a
n
a
n
+
1
}
的前n項和S_n．
（3）設
c
n
=
1
2
（
a
n
+
1
）
b
n
，記{c_n}的前n項和T_n.若t（n-1）²+2≤T_n對于n≥2且n∈N^*恒成立，求實數t的取值范圍．
組卷：390引用：1難度：0.5
解析
24．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，離心率為
1
2
，
A
1
，
A
2
分別為橢圓C的左、右頂點，過焦點且垂直于x軸的直線被橢圓C截得的線段長為3．
（1）求橢圓C的標準方程．
（2）當直線m過橢圓C的左焦點F₁以及上頂點P時，直線m與橢圓C交于另一點Q，求此時的弦長|PQ|．
（3）設直線l過點A₁，且與x軸垂直，M，N為直線l上關于x軸對稱的兩點，直線A₂M與橢圓C相交于異于A₂的點D，直線DN與x軸的交點為E，當△MA₂N與△MEN的面積之差取得最大值時，求直線A₂M的方程．
組卷：193引用：1難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（lnx）′=x	B．（ sin π 5 ） ′ = cos π 5
C．（cosx）′=sinx	D．（a^x）′=a^xlna（a＞0，a≠1）

2022-2023學年天津市濱海新區塘沽一中高二（上）期末數學試卷

一、選擇題（共12小題，每小題5分，滿分60分）

1．若直線過點（1，2），（4，2+3），則此直線的傾斜角是（ ）

2．三棱錐O-ABC中，M，N分別是AB，OC的中點，且OA=a，OB=b，OC=c，用a，b，c表示NM，則NM等于（ ）

3．設平面β的一個法向量為m=（2，-1，z），平面α的一個法向量為n=（4，-2，-2），若平面β⊥平面α，則實數z的值為（ ）

4．已知等差數列{an}的前n項和為Sn，且S21=21，則a6+a16的值為（ ）

5．下列求導運算正確的是（ ）

6．如圖，在直三棱柱ABC-A1B1C1中，已知AB⊥AC，D為CC1的中點，AB=AC=AA1，則AB1，A1D所成角的余弦值是（ ）

7．已知F1，F2是橢圓E：x28+y212=1的兩個焦點，過點F1且斜率為k的直線l與E交于M，N兩點，則△MNF2的周長為（ ）

8．已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的一條漸近線方程為y=255x,且與橢圓x215+y26=1有公共焦點，則C的方程為（ ）

三、解答題（共4小題，滿分50分）

1．若直線過點（1，2），（4，2+
3
），則此直線的傾斜角是（　　）

2．三棱錐O-ABC中，M，N分別是AB，OC的中點，且
OA
=
a
，
OB
=
b
，
OC
=
c
，用
a
，
b
，
c
表示
NM
，則
NM
等于（　　）

3．設平面β的一個法向量為
m
=
（
2
，-
1
，
z
）
，平面α的一個法向量為
n
=
（
4
，-
2
，-
2
）
，若平面β⊥平面α，則實數z的值為（　　）

4．已知等差數列{a_n}的前n項和為S_n，且S₂₁=21，則a₆+a₁₆的值為（　　）

5．下列求導運算正確的是（　　）

6．如圖，在直三棱柱ABC-A₁B₁C₁中，已知AB⊥AC，D為CC₁的中點，AB=AC=AA₁，則AB₁，A₁D所成角的余弦值是（　　）

7．已知F₁，F₂是橢圓E：
x
2
8
+
y
2
12
=1的兩個焦點，過點F₁且斜率為k的直線l與E交于M，N兩點，則△MNF₂的周長為（　　）

8．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線方程為y=
2
5
5
x,且與橢圓
x
2
15
+
y
2
6
=1有公共焦點，則C的方程為（　　）