2019-2020學年湖南省長沙市開福區北雅中學八年級（上）入學數學試卷

一、選擇題（在下列各題的四個選項中，只有一項是符合題意的.請在答題卡中填涂符合題意的選項，本題共12小題，每小題3分，共36分）

• 1．下列說法不正確的是（　　）

  A．0的平方根是0	B．1的算術平方根是1
  C．-1的立方根是±1	D．4的平方根是±2
  組卷：217引用：6難度：0.9

  解析

• 2．下列實數：3.1415926，

  3

  8

  ，0.1010010001…，

  4

  ，

  π

  3

  ，

  22

  7

  ，

  2

  1

  3

  其中無理數的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：28引用：1難度：0.9

  解析

• 3．以下問題，不適合用全面調查的是（　　）

  A．了解全班同學每周體育鍛煉的時間

  B．旅客上飛機前的安檢

  C．了解全市中小學生每天的零花錢

  D．學校招聘教師，對應聘人員面試
  組卷：41引用：3難度：0.9

  解析

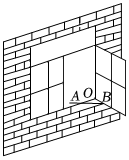• 4．如圖，一扇窗戶打開后，用窗鉤AB可將其固定，這里所運用的幾何原理是（　　）

  A．三角形的穩定性	B．兩點之間線段最短
  C．兩點確定一條直線	D．垂線段最短
  組卷：5268引用：162難度：0.9

  解析

• 5．若一個三角形的兩邊長分別為3和7，則第三邊長可能是（　　）

  A．6

  B．3

  C．2

  D．11
  組卷：6380引用：57難度：0.7

  解析

• 6．若一個正多邊形的一個內角等于150°，則這個正多邊形的邊數是（　　）

  A．9

  B．10

  C．11

  D．12
  組卷：481引用：12難度：0.9

  解析

• 7．為了了解某區20000名考生中考成績情況，有關部門從中抽取了500名考生的成績進行統計分析，在這個問題中（　　）

  A．20000名考生是總體

  B．20000名考生的中考成績是總體

  C．每名考生是個體

  D．500名考生是總體的一個樣本
  組卷：30引用：2難度：0.8

  解析

• 8．學校八年級師生共466人準備參加社會實踐活動．現已預備了49座和37座兩種客車共10輛，剛好坐滿．設49座客車x輛，37座客車y輛，根據題意可列出方程組（　　）

  A． x + y = 10 49 x + 37 y = 466	B． x + y = 10 37 x + 49 y = 466
  C． x + y = 466 49 x + 37 y = 10	D． x + y = 466 37 x + 49 y = 10
  組卷：1500引用：19難度：0.7

  解析

三、解答題（本題共8個小題，第19、20題每小題6分，第21、22題每小題6分，第23、24題每小題6分，第25、25題每小題6分，共66分.解答應寫出必要的文字說明、證明過程或演算步驟）

• 25．已知CD是經過∠BCA頂點C的一條直線，CA=CB．E、F分別是直線CD上兩點，且∠BEC=∠CFA=∠α．
  
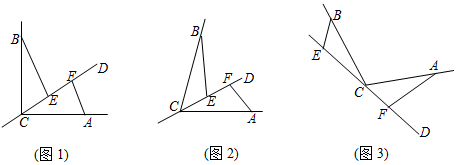
  （1）若直線CD經過∠BCA的內部，且E、F在射線CD上，請解決下面問題：
  ①如圖1，若∠BCA=90°，∠α=90°，探索三條線段EF、BE、AF的數量關系并證明你的結論；
  ②如圖2，若∠α+∠BCA=180°，請證明①中的結論仍然成立；
  （2）如圖3，若直線CD經過∠BCA的外部，∠α=∠BCA，請寫出三條線段EF、BE、AF的數量關系并證明你的結論．
  組卷：193引用：1難度：0.2

  解析

• 26．閱讀理解：我們把

  a	b
  c	d

  稱為二階行列式，規定它的運算法則為

  a	b
  c	d

  =ad-bc,例如：

  2	3
  4	5

  =2×5-3×4=-2．
  （1）填空：若

  - 1	2 x - 1
  0 . 5	x

  =0，則x=

  ，

  2	1
  3 - x	x

  ＞0，則x的取值范圍

  ；
  （2）若對于正整數m,n滿足，1

  ＜

  1	n
  m	4

  ＜3，求m+n的值；
  （3）若對于兩個非負數x,y,

  x - 1	y
  2	3

  =

  x	- y
  2	- 1

  =k-1，求實數k的取值范圍．
  組卷：901引用：5難度：0.6

  解析