當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省南京一中高三（上）期中數學試卷

發布：2024/11/18 3:30:2

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．設全集U=R，集合A={x|x＞0}，B={x|x＜2}，則圖中陰影部分表示的集合為（　　）
A．（0，+∞） B．（0，2）
C．[2，+∞） D．（-∞，0）∪[2，+∞）
組卷：23引用：4難度：0.8
解析
2．已知i為虛數單位，復數
z
=
3
-
i
1
-
i
，則|z²|=（　　）
A．3 B．4 C．5 D．25
組卷：47引用：3難度：0.8
解析
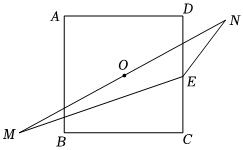3．如圖，在邊長為2的正方形ABCD中，其對稱中心O平分線段MN，且MN=2BC，點E為DC的中點，則
EM
?
EN
=（　　）
A．-3 B．-2 C．-
3
2
D．-
1
2
組卷：145引用：7難度：0.7
解析
4．2012年國家開始實施法定節假日高速公路免費通行政策，某收費站統計了2021年中秋節前后車輛通行數量，發現該站近幾天車輛通行數量ξ～N（1000，σ²），若P（ξ＞1200）=a,P（800＜ξ＜1200）=b,則當8ab≥b+2a時下列說法正確的是（　　）
A．
a
=
1
2
B．
b
=
1
4
C．
a
+
b
=
3
4
D．
a
-
b
=
1
2
組卷：149引用：3難度：0.7
解析
5．已知等比數列{a_n}的前n項和為S_n，且a₂，3a₅，9a₈成等差數列，則
S
6
S
3
=（　　）
A．
1
3
B．
4
3
C．3 D．4
組卷：502引用：9難度：0.7
解析
6．已知F是雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點，O為坐標原點，y=kx與雙曲線C交于M（M在第一象限），N兩點，3|MF]=|NF|，且
∠
MFN
=
2
π
3
，則該雙曲線的離心率為（　　）
A．
2
B．
3
C．
7
D．
7
2
組卷：272引用：5難度：0.5
解析
7．甲、乙、丙、丁、戊共5名同學進行勞動技術比賽，決出第1名到第5名的名次．甲和乙去詢問成績，回答者對甲說：“很遺憾，你和乙都沒有獲得冠軍．”對乙說：“你當然不會是最差的．”若在此對話的基礎上5人名次的情況是等可能的，則最終丙和丁獲得前兩名的概率為（　　）
A．
4
27
B．
8
27
C．
2
9
D．
4
9
組卷：91引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分．解答時應寫出必要的文字說明、證明過程或演算步驟．

21．在平面直角坐標系xOy中：
①已知點A（
3
，0），直線
l
：
x
=
4
3
3
，動點P滿足到點A的距離與到直線l的距離之比
3
2
；
②已知點S，T分別在x軸，y軸上運動，且|ST|=3，動點P滿
OP
=
2
3
OS
+
1
3
OT
；
③已知圓C的方程為x²+y²=4，直線l為圓C的切線，記點
A
（
3
，
0
）
，
B
（
-
3
，
0
）
到直線l的距離分別為d₁，d₂，動點P滿足|PA|=d₁，|PB|=d₂．
（Ⅰ）在①，②，③這三個條件中任選一個，求動點P的軌跡方程；
（Ⅱ）記（Ⅰ）中動點P的軌跡為E，經過點D（1，0）的直線l′交E于M，N兩點，若線段MN的垂直平分線與y軸相交于點Q，求點Q縱坐標的取值范圍．
組卷：224引用：3難度：0.4
解析
22．函數
f
（
x
）
=
1
m
e
mx
-
1
2
x
2
，f'（x）是f（x）的導函數．
（1）若m=1，x∈R，求函數g（x）=f（x）+f（-x）的最小值．
（2）對?x∈（e,+∞），且m＞1，證明：
mx
（
mx
-
6
）
+
2
f
′
（
x
）
lnx
≥
lnx
-
6
恒成立．
組卷：125引用：4難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（0，+∞）	B．（0，2）
C．[2，+∞）	D．（-∞，0）∪[2，+∞）

2022-2023學年江蘇省南京一中高三（上）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．設全集U=R，集合A={x|x＞0}，B={x|x＜2}，則圖中陰影部分表示的集合為（ ）

2．已知i為虛數單位，復數z=3-i1-i，則|z2|=（ ）

3．如圖，在邊長為2的正方形ABCD中，其對稱中心O平分線段MN，且MN=2BC，點E為DC的中點，則EM?EN=（ ）

5．已知等比數列{an}的前n項和為Sn，且a2，3a5，9a8成等差數列，則S6S3=（ ）

6．已知F是雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的右焦點，O為坐標原點，y=kx與雙曲線C交于M（M在第一象限），N兩點，3|MF]=|NF|，且∠MFN=2π3，則該雙曲線的離心率為（ ）

四、解答題：本題共6小題，共70分．解答時應寫出必要的文字說明、證明過程或演算步驟．

22．函數f（x）=1memx-12x2，f'（x）是f（x）的導函數．（1）若m=1，x∈R，求函數g（x）=f（x）+f（-x）的最小值．（2）對?x∈（e,+∞），且m＞1，證明：mx（mx-6）+2f′（x）lnx≥lnx-6恒成立．

1．設全集U=R，集合A={x|x＞0}，B={x|x＜2}，則圖中陰影部分表示的集合為（　　）

2．已知i為虛數單位，復數
z
=
3
-
i
1
-
i
，則|z²|=（　　）

3．如圖，在邊長為2的正方形ABCD中，其對稱中心O平分線段MN，且MN=2BC，點E為DC的中點，則
EM
?
EN
=（　　）

5．已知等比數列{a_n}的前n項和為S_n，且a₂，3a₅，9a₈成等差數列，則
S
6
S
3
=（　　）

6．已知F是雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點，O為坐標原點，y=kx與雙曲線C交于M（M在第一象限），N兩點，3|MF]=|NF|，且
∠
MFN
=
2
π
3
，則該雙曲線的離心率為（　　）

22．函數
f
（
x
）
=
1
m
e
mx
-
1
2
x
2
，f'（x）是f（x）的導函數．
（1）若m=1，x∈R，求函數g（x）=f（x）+f（-x）的最小值．
（2）對?x∈（e,+∞），且m＞1，證明：
mx
（
mx
-
6
）
+
2
f
′
（
x
）
lnx
≥
lnx
-
6
恒成立．