2022-2023學年山東省青島五十九中八年級（下）期中數學試卷
發布：2024/4/20 14:35:0
一、選擇題（本題共8小題，每題3分，共24分）
-
1．下列圖形是中心對稱圖形而不是軸對稱圖形的是（ ）
組卷：155引用：5難度：0.8 -
2．下列判斷錯誤的是（ ）
組卷：250引用：2難度：0.7 -
3．下列等式中，從左到右的變形是因式分解的是（ ）
組卷：3351引用：33難度：0.7 -
4．在數軸上表示不等式組
的解集，正確的是（ ）x≥-2x＜4組卷：650引用：35難度：0.9 -
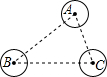5．如圖，A，B，C表示三個居民小區，為豐富居民們的文化生活，現準備建一個文化廣場，使它到三個小區的距離相等，則文化廣場應建在（ ）組卷：1599引用：32難度：0.9 -
6．如圖，在Rt△ABC中，∠ABC=90°，AB=BC=，將△ABC繞點C逆時針旋轉60°，得到△MNC，連接BM，則BM的長是（ ）2組卷：477引用：3難度：0.6 -
7．如圖，直線y=kx+b與坐標軸的兩交點分別為A（2，0）和B（0，-3），則不等式kx+b+3≤0的解集為（ ）組卷：1580引用：9難度：0.9 -
8．如圖，在正方形網格中，格點△ABC繞某點順時針旋轉角α（0＜α＜180°）得到格點△A1B1C1，點A與點A1，點B與點B1，點C與點C1是對應點，則α=（ ）組卷：377引用：5難度：0.6
三、解答題（本題滿分0分）
-
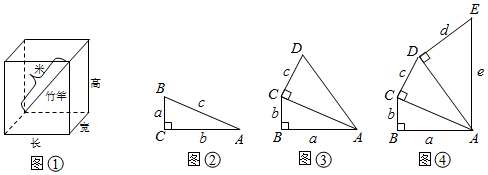
24．【實際問題】小明家住16樓．一天，他要把一根3米長的竹竿放入電梯帶回家中．如果竹竿恰好剛能放入電梯中（如圖①示），那么，電梯的長、寬、高和的最大值是多少米？
【類比探究】為了解決這個實際問題，我們首先探究下面的數學問題．
探究1：如圖②，在△ABC中，AC⊥BC．若BC=a,AC=b,AB=c,則b與c之間有什么數量關系？
解：在△ABC中，∵AC⊥BC，
∴BC2+AC2=AB2，即a2+b2=c2．
∵（a-b）2≥0，
∴a2+b2-2ab≥0．
∴a2+b2≥2ab.
∴c2≥2ab.
∴c2+a2+b2≥2ab+a2+b2．
∴2c2≥（a+b）2．
∵a,b,c均大于0，
∴a+b與c之間的數量關系是a+b≤c.2
探究2：如圖③，在四邊形ABCD中，AC是對角線，AB⊥BC，AC⊥CD．若AB=a,BC=b,CD=c,AD=d,則a+b+c與d之間有什么數量關系？
解：∵AB⊥BC，AC⊥CD，
∴BC2+AB2=AC2，AC2+CD2=AD2．
∴a2+b2+c2=d2．
∵（a-b）2≥0，（a-c）2≥0，（b-c）2≥0，
∴a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc.
將上面三式相加得，2a2+2b2+2c2≥2ab+2ac+2bc,
∴2d2≥2ab+2ac+2bc.
∴2d2+a2+b2+c2≥2ab+2ac+2bc+a2+b2+c2．
∴d2≥（a+b+c）2．
∵a,b,c,d均大于0，
∴a+b+c與d之間有這樣的數量關系：a+b+c≤d.
探究3：如圖④，仿照上面的方法探究，在五邊形ABCDE中，AC，AD是對角線，AB⊥BC，AC⊥CD，AD⊥DE．若AB=a,BC=b,CD=c,DE=d,AE=e,則a+b+c+d與e之間的數量關系是 ．
【歸納結論】
當a1＞0，a2＞0，…，an＞0，m＞0時，若a12+a22+…+an2=m2，則a1+a2+…+an與m之間的數量關系是 ．
【問題解決】
小明家住16樓．一天，他要把一根3米長的竹竿放入電梯帶回家中．如果竹竿恰好剛能放入電梯中（如圖①示），那么，電梯的長、寬、高和的最大值是 米．
【拓展延伸】
公園準備修建一個四邊形水池，邊長分別為a米，b米，c米，d米．分別以水池四邊為邊向外建四個正方形花園，若花園面積和為400平方米，則水池的最大周長為 米．組卷：652引用：4難度：0.2 -
25．已知△ABC是等邊三角形，點P為射線AD上任意一點（點P與點A不重合）．連接CP，將線段CP繞點C順時針旋轉60°得到線段CQ，連接QB并延長交直線AD于點E．
（1）如圖1．當∠DAC=90°時，試猜想BC與QE的位置關系，并說明理由．
（2）如圖2．當∠DAC是銳角時．求∠QEP的度數．
（3）如圖3．當∠DAC=120°，且∠ACP=15°，點E恰好與點A重合．若AC=6．求BQ的長．組卷：642引用：5難度：0.1