2022-2023學年天津市西青區楊柳青一中高二（下）第三次適應性數學試卷

一、選擇題：本大題共9小題，每小題5分，共計45分，每小題有且僅有一項符合題目要求.

• 1．已知集合U={1，2，3，4，5，6}，A={x∈Z|2≤x＜6}，B={1，2，4，6}，則A∩（?_UB）=（　　）

  A．{2}

  B．{3，5}

  C．{1，4，6}

  D．{2，3，5}
  組卷：465引用：4難度：0.7

  解析

• 2．設x∈R，則“

  2

  x

  ＜

  1

  4

  ”是“x²+x-2＞0”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：211引用：6難度：0.5

  解析

• 3．已知拋物線C₁：x²=2py（p＞0）的焦點為F，雙曲線C₂：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的離心率為

  3

  ，F到雙曲線C₂的漸近線的距離為2，則拋物線C₁的方程為（　　）

  A． x 2 = 4 3 y

  B． x 2 = 8 3 y

  C． x 2 = 4 6 y

  D． x 2 = 8 6 y
  組卷：355引用：3難度：0.7

  解析

• 4．已知

  2

  x

  =

  3

  ，

  lo

  g

  2

  8

  9

  =

  y

  ，則2x+y=（　　）

  A．3

  B．5

  C．2log23

  D．23
  組卷：1051引用：3難度：0.8

  解析

• 5．函數

  f

  （

  x

  ）

  =

  ln

  |

  x

  |

  ?

  cosx

  x

  +

  sinx

  在[-π，0）∪（0，π]的圖象大致為（　　）

  A．

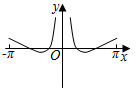
  B．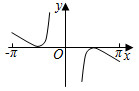

  C．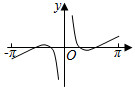

  D．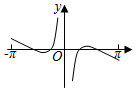
  組卷：678引用：21難度：0.9

  解析

• 6．已知三棱柱ABC-A₁B₁C₁的側棱垂直于底面，各頂點都在同一球面上，若該棱柱的體積為

  3

  ，AB=2，AC=1，AC⊥BC，則此球的表面積等于（　　）

  A．8π

  B．9π

  C．10π

  D．11π
  組卷：104引用：1難度：0.6

  解析

三、解答題：本大題共3小題，共45分，解答應寫出文字說明，證明過程或演算步驟.

• 18．設{a_n}是首項為1的等比數列，且滿足a₁，3a₂，9a₃成等差數列，等差數列{b_n}前n項和為S_n，公差為1，且滿足S₈=36．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）求數列{（-1）ⁿa_nb_n}的前2n項的和T_2n；
  （3）設c_n=

  （ 4 b n + 5 ） a n + 1 b n - 1 b n + 1 ， n 為偶數

  （ - 1 ） n + 1 2 b 2 n ， n 為奇數

  ，求數列{c_n}的前2n項和Q_2n．
  組卷：147引用：2難度：0.4

  解析

三、附加題：

• 19．將函數

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  π

  3

  ）

  （

  0

  ＜

  ω

  ＜

  1

  ）

  的圖象向左平移

  π

  2

  個單位長度后得到曲線C，若曲線C關于y軸對稱，則曲線C的一個對稱中心為

  ．
  組卷：68引用：3難度：0.6

  解析