2022-2023學年河北省保定市高三(上)摸底數學試卷
發布:2024/4/20 14:35:0
一、選擇題。本題共8小題,每小題5分,共40分。在每小題給出的四個選項中,只有一項是符合題目要求的。
-
1.若集合M={x|-1<2-x≤1},N={1,2,3},則M∩N=( )
A.{2,3} B.[1,2] C.[2,3] D.{1,2} 組卷:5引用:2難度:0.7 -
2.若復數z滿足(z-1)?i=4(1-i),則|z|=( )
A.1 B.3 C.5 D.7 組卷:38引用:2難度:0.8 -
3.如果
,a是兩個共線的單位向量,則( )bA. =abB. ?a=0bC. ?a=1bD. 2=a2b組卷:71引用:1難度:0.7 -
 4.我國古代數學名著《九章算術》對立體幾何有著深入的研究,從其中的一些數學用語可見,譬如“塹堵”指底面為直角三角形且側棱垂直于底面的三棱柱,“陽馬”指底面是矩形且有一側棱垂直于底面的四棱錐,“鱉臑”指的是四個面都是直角三角形的三棱錐.現有一如圖所示的“塹堵”ABC-A1B1C1,其中AC⊥BC,若AA1=AB=2,則“陽馬”B-A1ACC1的體積最大為( )
4.我國古代數學名著《九章算術》對立體幾何有著深入的研究,從其中的一些數學用語可見,譬如“塹堵”指底面為直角三角形且側棱垂直于底面的三棱柱,“陽馬”指底面是矩形且有一側棱垂直于底面的四棱錐,“鱉臑”指的是四個面都是直角三角形的三棱錐.現有一如圖所示的“塹堵”ABC-A1B1C1,其中AC⊥BC,若AA1=AB=2,則“陽馬”B-A1ACC1的體積最大為( )A. 23B.2 C. 43D.4 組卷:74引用:4難度:0.6 -
5.等差數列{an}中,a4,a2019是方程x2-4x+3=0的兩個根,則{an}的前2022項和為( )
A.1011 B.2022 C.4044 D.8088 組卷:84引用:3難度:0.7 -
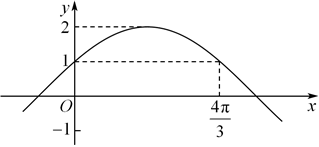 6.已知函數的部分圖象如圖所示,則函數f(x)的單調遞增區間是( )f(x)=2sin(ωx+φ)(ω>0,0<φ<π2)
6.已知函數的部分圖象如圖所示,則函數f(x)的單調遞增區間是( )f(x)=2sin(ωx+φ)(ω>0,0<φ<π2)A. [-4π3+2kπ,2π3+2kπ](k∈Z)B. [-4π3+4kπ,2π3+4kπ](k∈Z)C. [-π3+2kπ,2π3+2kπ](k∈Z)D. [-5π3+4kπ,2π3+4kπ](k∈Z)組卷:49引用:2難度:0.5 -
7.已知x>0,函數f(x)=2x+x-5,g(x)=x2+x-4,h(x)=log2x+x-3的零點分別為a,b,c,則( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a 組卷:42引用:2難度:0.7
四、解答題。本題共6小題,共70分。解答應寫出文字說明、證明過程或演算步驟。
-
21.某公司出產了一款美觀實用的筷子籠,如圖,是由與圓柱底面成一定角度的截面截圓柱所得.如果從截面的最底端到最高端部分還原圓柱,如圖所示,AB,A'B'分別為圓柱OO'底面直徑,AA',BB'為圓柱的母線,AB=AA'=2,過AB'的平面α截圓柱且與底面所在平面交于直線l,且AB⊥l.
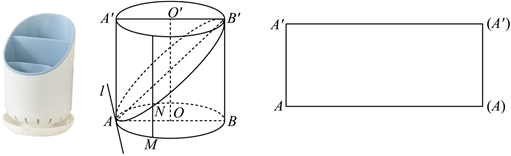
(1)證明:l⊥AB';
(2)若底面有一動點M從A點出發在圓O上運動,過動點M的母線與截面α交于點N,設,MN=y,其中x∈[0,2π).?AM=x
①求y與x的函數關系;
②將圓柱OO'側面沿母線AA'剪開并展平,請在所給的展開圖中畫出平面α截圓柱側面的截痕,并建立適當的平面直角坐標系直接寫出其解析式.組卷:9引用:2難度:0.5 -
22.已知函數f(x)=alnx-x.
(1)討論f(x)的單調性;
(2)設x1,x2是f(x)的兩個不同零點,且x1<x2,證明:2lnx1+lnx2>e.組卷:52引用:2難度:0.5


