2021-2022學年山東省德州九中八年級（下）期中數學試卷

一、選擇題（本大題共12小題，共48.0分）

• 1．下列各式中，一定是二次根式的是（　　）

  A． - - 2

  B． 3 3

  C． a - 1

  D． a 2 + 1
  組卷：447引用：4難度：0.8

  解析

• 2．下列運算正確的是（　　）

  A． 3 + 2 = 5

  B． 3 × 2 = 6

  C．（ 3 -1）2=3-1

  D． 5 2 - 3 2 =5-3
  組卷：565引用：82難度：0.9

  解析

• 3．如圖，矩形ABCD中，AB=3，AD=1，AB在數軸上，若以點A為圓心，對角線AC的長為半徑作弧交數軸于點M，則點M表示的數為（　　）

  A．2

  B． 5 - 1

  C． 10 - 1

  D． 5
  組卷：3295引用：50難度：0.9

  解析

• 4．下列命題，其中是真命題的為（　　）

  A．一組對邊平行，另一組對邊相等的四邊形是平行四邊形

  B．對角線互相垂直的四邊形是菱形

  C．對角線相等的四邊形是矩形

  D．一組鄰邊相等的矩形是正方形
  組卷：2159引用：49難度：0.7

  解析

• 5．我們知道：四邊形具有不穩定性．如圖，在平面直角坐標系中，邊長為2的正方形ABCD的邊AB在x軸上，AB的中點是坐標原點O，固定點A，B，把正方形沿箭頭方向推，使點D落在y軸正半軸上點D′處，則點C的對應點C′的坐標為（　　）

  A．（ 3 ，1）

  B．（2，1）

  C．（1， 3 ）

  D．（2， 3 ）
  組卷：6599引用：103難度：0.7

  解析

• 6．古希臘幾何學家海倫和我國宋代數學家秦九韶都曾提出利用三角形的三邊求面積的公式，稱為海倫-秦九韶公式：如果一個三角形的三邊長分別是a,b,c,記p=

  a

  +

  b

  +

  c

  2

  ，那么三角形的面積為S=

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ．如圖，在△ABC中，∠A，∠B，∠C所對的邊分別記為a,b,c,若a=5，b=6，c=7，則△ABC的面積為（　　）

  A．6 6

  B．6 3

  C．18

  D． 19 2
  組卷：1604引用：23難度：0.8

  解析

• 7．為考查兩名實習工人的工作情況，質檢部將他們工作第一周每天生產合格產品的個數整理成甲、乙兩組數據，如下表：

  甲	2	6	7	7	8
  乙	2	3	4	8	8

  關于以上數據，說法正確的是（　　）

  A．甲、乙的眾數相同

  B．甲、乙的中位數相同

  C．甲的平均數小于乙的平均數

  D．甲的方差小于乙的方差
  組卷：1217引用：30難度：0.7

  解析

• 8．在△ABC中，點D是邊BC上的點（與B，C兩點不重合），過點D作DE∥AC，DF∥AB，分別交AB，AC于E，F兩點，下列說法正確的是（　　）

  A．若AD⊥BC，則四邊形AEDF是矩形

  B．若AD垂直平分BC，則四邊形AEDF是矩形

  C．若BD=CD，則四邊形AEDF是菱形

  D．若AD平分∠BAC，則四邊形AEDF是菱形
  組卷：6976引用：59難度：0.7

  解析

三、解答題（本大題共7小題，共78.0分）

• 24．如圖，菱形ABCD中，分別延長DC，BC至點E，F，使CE=CD，CF=CB，連接DB，BE，EF，FD．
  （1）求證：四邊形DBEF是矩形；
  （2）如果∠A=60°，菱形ABCD的面積為

  8

  3

  ，求DF的長．
  組卷：1166引用：12難度：0.7

  解析

• 25．如圖1，四邊形ABCD是正方形，點E是邊BC的中點，∠AEF=90°，且EF交正方形外角平分線CF于點F．
  （1）求證：AE=EF；
  （2）如圖2，若把條件“點E是邊BC的中點”改為“點E是邊BC上的任意一點”，其余條件不變，（1）中的結論是否仍然成立？

  ；（填“成立”或“不成立”）；
  （3）如圖3，若把條件“點E是邊BC的中點”改為“點E是邊BC延長線上的一點”，其余條件仍不變，那么結論AE=EF是否成立呢？若成立請證明，若不成立說明理由．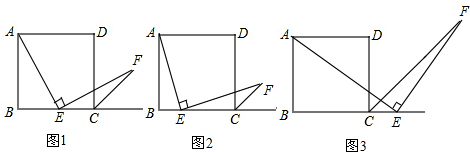
  
  組卷：677引用：7難度：0.5

  解析