2006年全國初中數學競賽（海南賽區）試卷

一、選擇題（共10小題，每小題5分，滿分50分）

• 1．式子（-1）²⁰⁰⁵+（-1）²⁰⁰⁶的值是（　　）

  A．-1

  B．1

  C．-2

  D．0
  組卷：120引用：7難度：0.9

  解析

• 2．若實數a,b滿足ab=1，設M=

  a

  a

  +

  1

  +

  b

  b

  +

  1

  ，N=

  1

  a

  +

  1

  +

  1

  b

  +

  1

  ，則M，N的大小關系是（　　）

  A．M＞N

  B．M=N

  C．M＜N

  D．不確定
  組卷：3572引用：38難度：0.5

  解析

• 3．分別表示三種不同的物體，如圖所示，前兩架天平保持平衡，如果要使第三架天平也平衡，那么“？”處應放“”的個數為（　　）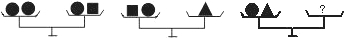
  

  A．2

  B．3

  C．4

  D．5
  組卷：595引用：37難度：0.9

  解析

• 4．甲、乙兩超市為了促銷一種定價相同的商品，甲超市連續兩次降價10%，乙超市一次性降價20%，在哪家超市購買此種商品更合算（　　）

  A．甲	B．乙
  C．同樣	D．與商品的價格有關
  組卷：766引用：42難度：0.9

  解析

• 5．根據下列表格的對應值，判斷方程ax²+bx+c=0（a≠0，a、b、c為常數）一個解的范圍是（　　）
  

  x	3.23	3.24	3.25	3.26
  ax2+bx+c	-0.06	-0.02	0.03	0.09

  A．3＜x＜3.23	B．3.23＜x＜3.24
  C．3.24＜x＜3.25	D．3.25＜x＜3.26
  組卷：3550引用：211難度：0.9

  解析

• 6．在平面直角坐標系中，已知A（2，-2），點P是y軸上一點，則使AOP為等腰三角形的點P有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：1820引用：19難度：0.9

  解析

三、解答題（共3小題，滿分35分）

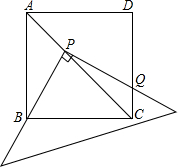• 19．如圖，將一三角板放在邊長為1的正方形ABCD上，并使它的直角頂點P在對角線AC上滑動，直角的一邊始終經過點B，另一邊與射線DC相交于Q．
  探究：設A、P兩點間的距離為x.
  （1）當點Q在邊CD上時，線段PQ與PB之間有怎樣的數量關系？試證明你的猜想；
  （2）當點Q在邊CD上時，設四邊形PBCQ的面積為y,求y與x之間的函數關系，并寫出函數自變量x的取值范圍；
  （3）當點P在線段AC上滑動時，△PCQ是否可能成為等腰三角形？如果可能，指出所有能使△PCQ成為等腰三角形的點Q的位置．并求出相應的x值，如果不可能，試說明理由．
  組卷：2793引用：19難度：0.5

  解析

• 20．已知A，A是拋物線y=

  1

  2

  x²上兩點，A₁B₁，A₃B₃分別垂直于x軸，垂足分別為B₁，B₃，點C是線段A₁A₃的中點，過點C作CB₂垂直于x軸，垂足為B₂，CB₂交拋物線于點A₂．
  
  （1）如圖1，已知A₁，A₃兩點的橫坐標依次為1，3，求線段CA₂的長；
  （2）如圖2，若將拋物線y=

  1

  2

  x²改為拋物線y=

  1

  2

  x²-x+1，且A₁，A₂，A₃三點的橫坐標為連續的整數，其他條件不變，求線段CA₂的長；
  （3）若將拋物線y=

  1

  2

  x²改為拋物線y=ax²+bx+c（a＞0），A₁，A₂，A₃三點的橫坐標為連續整數，其他條件不變，試猜想線段CA₂的長（用a,b,c表示，并直接寫出答案）．
  組卷：95引用：4難度：0.1

  解析