2022-2023學年江西省上饒市廣豐區重點高中高二（上）期中數學試卷

一、單選題

• 1．已知A（3，3，3），B（6，6，6），O為原點，則

  OA

  與

  BO

  的夾角是（　　）

  A．0

  B．π

  C． 3 π 2

  D．2π
  組卷：108引用：5難度：0.7

  解析

• 2．若拋物線y²=2px（p＞0）的焦點到直線y=x+1的距離為

  2

  ，則p=（　　）

  A．1

  B．2

  C．2 2

  D．4
  組卷：4920引用：17難度：0.7

  解析

• 3．已知正方體ABCD-A₁B₁C₁D₁的棱長為a,則平面AB₁D₁與平面BC₁D的距離為（　　）

  A． 2 a 3

  B． 2 a 2

  C． 3 a 3

  D． 3 a 2
  組卷：75引用：6難度：0.7

  解析

• 4．設B是橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的上頂點，若C上的任意一點P都滿足|PB|≤2b,則C的離心率的取值范圍是（　　）

  A．[ 2 2 ，1）

  B．[ 1 2 ，1）

  C．（0， 2 2 ]

  D．（0， 1 2 ]
  組卷：6091引用：19難度：0.6

  解析

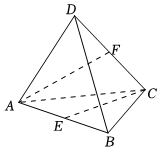• 5．已知四面體ABCD，所有棱長均為2，點E，F分別為棱AB，CD的中點，則

  AF

  ?

  CE

  =（　　）

  A．1

  B．2

  C．-1

  D．-2
  組卷：1152引用：9難度：0.6

  解析

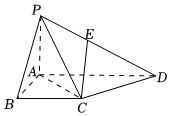• 6．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，PB與底面ABCD所成的角為

  π

  4

  ，底面ABCD為直角梯形，

  ∠

  ABC

  =∠

  BAD

  =

  π

  2

  ，

  AD

  =

  2

  ，

  PA

  =

  BC

  =

  1

  ，點E為棱PD上一點，滿足

  PE

  =

  λ

  PD

  （

  0

  ≤

  λ

  ≤

  1

  ）

  ，下列結論錯誤的是（　　）

  A．平面PAC⊥平面PCD

  B．點P到直線CD的距離 3

  C．若二面角E-AC-D的平面角的余弦值為 3 3 ，則 λ = 1 3

  D．點A到平面PCD的距離為 5 2
  組卷：318引用：3難度：0.5

  解析

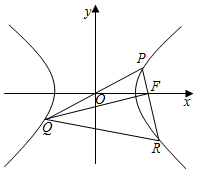• 7．如圖，O是坐標原點，P是雙曲線

  E

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  右支上的一點，F是E的右焦點，延長PO，PF分別交E于Q，R兩點，已知QF⊥FR，且|QF|=2|FR|，則E的離心率為（　　）

  A． 17 4

  B． 17 3

  C． 21 4

  D． 21 3
  組卷：638引用：11難度：0.5

  解析

四、解答題

• 21．在①離心率

  e

  =

  1

  2

  ，②橢圓C過點

  （

  1

  ，

  3

  2

  ）

  ，③△PF₁F₂面積的最大值為

  3

  ，這三個條件中任選一個，補充在下面（橫線處）問題中，解決下面兩個問題．
  設橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁、F，過F₁且斜率為k的直線l交橢圓于P、Q兩點，已知橢圓C的短軸長為

  2

  3

  ，_____．
  （1）求橢圓C的方程；
  （2）若線段PQ的中垂線與x軸交于點N，求證：

  |

  PQ

  |

  |

  N

  F

  1

  |

  為定值．
  組卷：256引用：8難度：0.5

  解析

• 22．已知動點Q到直線x=-2的距離比到定點（1，0）的距離大1．
  （Ⅰ）寫出動點Q的軌跡C的方程；
  （Ⅱ）設x=my+1為過（1，0）作曲線C的任一條弦AB所在直線方程，弦AB的中點為D，過D點作直線DP與直線x=-1交于點P，與x軸交于點M，且使得|PA|=|PB|，|PD|=|AB|，求∠PMF的正弦值（其中F為定點（1，0））．
  組卷：32引用：2難度：0.5

  解析