2021-2022學(xué)年廣東省佛山市南海中學(xué)高一（上）期中數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．已知集合A={-1，0，1，2}，B={x|0＜x＜3}，則圖中陰影部分表示的集合為（　　）

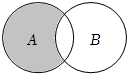
  A．{-1}

  B．{-1，0}

  C．{1，2}

  D．{0，1，2}
  組卷：127引用：2難度：0.9

  解析

• 2．設(shè)命題p：?x≥1，x²≥1，則p的否定為（　　）

  A．?x≥1，x2＜1

  B．?x＜1，x2＜1

  C．?x≥1，x2＜1

  D．?x＜1，x2＜1
  組卷：38引用：6難度：0.7

  解析

• 3．函數(shù)f（x）=

  2

  x

  -

  1

  +

  1

  x

  -

  2

  的定義域?yàn)椋ā　。?/h2>

  A．[0，2）	B．（2，+∞）
  C．[ 1 2 ，2）∪（2，+∞）	D．（-∞，2）∪（2，+∞）
  組卷：435引用：32難度：0.9

  解析

• 4．下列四組函數(shù)中，表示同一函數(shù)的一組是（　　）

  A．f（x）=x0，g（x）=1

  B． y = x , u = （ v ） 2

  C． f （ x ） = x 2 - 1 x - 1 ， g （ t ） = t + 1

  D． f （ x ） = 1 + x ? 1 - x ， g （ x ） = 1 - x 2
  組卷：50引用：2難度：0.7

  解析

• 5．設(shè)a,b,c是實(shí)數(shù)，則“a＞b”是“ac²＞bc²”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：328引用：16難度：0.8

  解析

• 6．若定義在R上的偶函數(shù)f（x）在（-∞，0]上單調(diào)遞增，且f（-2）=0，則滿(mǎn)足xf（x）＜0的x的取值范圍是（　　）

  A．（-∞，-2）∪（0，2）	B．（-2，0）∪（2，+∞）
  C．（-∞，-2）∪（2，+∞）	D．（-2，2）
  組卷：67引用：5難度：0.7

  解析

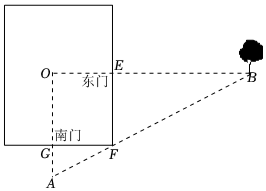• 7．《九章算術(shù)》是中國(guó)傳統(tǒng)數(shù)學(xué)最重要的著作，奠定了中國(guó)傳統(tǒng)數(shù)學(xué)的基本框架，其中卷第九勾股中記載：“今有邑，東西七里，南北九里，各中開(kāi)門(mén)．出東門(mén)一十五里有木．問(wèn)出南門(mén)幾何步而見(jiàn)木？”其算法為：東門(mén)南到城角的步數(shù)，乘南門(mén)東到城角的步數(shù)，乘積作被除數(shù)，以樹(shù)距離東門(mén)的步數(shù)作除數(shù)，被除數(shù)除以除數(shù)得結(jié)果，即出南門(mén)x里見(jiàn)到樹(shù)，則x=

  （

  9

  ×

  1

  2

  ）

  ×

  （

  7

  ×

  1

  2

  ）

  15

  ．若一小城，如圖所示，出東門(mén)1200步有樹(shù)，出南門(mén)750步能見(jiàn)到此樹(shù)，則該小城的周長(zhǎng)的最小值為（　　）（注：1里=300步）

  A． 2 10 里

  B． 4 10 里

  C． 6 10 里

  D． 8 10 里
  組卷：78引用：11難度：0.6

  解析

四、解答題：本題共6小題，共70分，解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．已知二次函數(shù)f（x）是R上的偶函數(shù)，且f（0）=4，f（1）=5．
  （1）求函數(shù)f（x）的解析式；
  （2）設(shè)

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  x

  ，根據(jù)函數(shù)單調(diào)性的定義證明g（x）在區(qū)間（2，+∞）上單調(diào)遞增；
  （3）當(dāng)a＞0時(shí)，解關(guān)于x的不等式f（x）＞（1-a）x²+2（a+1）x.
  組卷：54引用：1難度：0.4

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  x

  2

  -

  1

  x

  2

  ．
  （1）判斷函數(shù)f（x）的奇偶性并證明；
  （2）若不等式x²f（x）+1-kx≥x³對(duì)任意

  x

  ∈

  [

  1

  4

  ，

  1

  ]

  都成立，求實(shí)數(shù)k的取值范圍；
  （3）當(dāng)

  x

  ∈

  [

  1

  m

  ，

  1

  n

  ]

  （

  m

  ＞

  0

  ，

  n

  ＞

  0

  ）

  時(shí)，函數(shù)g（x）=tf（x）+1（t＞0）的值域?yàn)閇2-3m,2-3n]，求實(shí)數(shù)t的取值范圍．
  組卷：33引用：1難度：0.4

  解析