2022-2023學年浙江省嘉興一中高二（上）期中數學試卷

一、單選題（共40分）

• 1．已知方程x²+y²-2x+2+3k=0表示圓，則k的取值范圍是（　　）

  A．（-∞，-1）	B． （ - ∞ ，- 1 3 ）
  C．（-∞，-1）∪（3，+∞）	D． （ - 3 2 ， + ∞ ）
  組卷：135引用：2難度：0.8

  解析

• 2．若直線ax-y+c=0經過第一、二、四象限，則有（　　）

  A．a＞0，c＞0

  B．a＞0，c＜0

  C．a＜0，c＞0

  D．a＜0，c＜0
  組卷：187引用：5難度：0.8

  解析

• 3．用數學歸納法證明“

  1

  n

  +

  1

  +

  1

  n

  +

  2

  +

  1

  n

  +

  3

  +?+

  1

  3

  n

  +

  1

  ＞1”時，假設n=k時命題成立，則當n=k+1時，左端增加的項為（　　）

  A． 1 3 k + 1	B． 1 3 k + 1 - 1 k + 1
  C． 1 3 k + 2 + 1 3 k + 3 + 1 3 k + 4	D． 1 3 k + 2 + 1 3 k + 4 - 2 3 （ k + 1 ）
  組卷：166引用：2難度：0.7

  解析

• 4．“中國剩余定理”又稱“孫子定理”，1852年英國來華傳教士偉烈亞力將《孫子算經》中“物不知數”問題的解法傳至歐洲．1874年，英國數學家馬西森指出此法符合1801年由高斯得出的關于同余式解法的一般性定理，因而西方稱之為“中國剩余定理”．“中國剩余定理”講的是一個關于整除的問題，現有這樣一個整除問題：將正整數中能被3除余2且被7除余2的數按由小到大的順序排成一列，構成數列{a_n}，則a₆=（　　）

  A．17

  B．37

  C．107

  D．128
  組卷：46引用：4難度：0.7

  解析

• 5．已知數列{a_n}滿足：

  a

  n

  =

  （ 3 - a ） n - 8 ， n ≤ 6

  a n - 6 ， n ＞ 6

  （n∈N^*），且數列{a_n}是遞增數列，則實數a的取值范圍是（　　）

  A．（2，3）

  B．[2，3）

  C． （ 10 7 ， 3 ）

  D．（1，3）
  組卷：217引用：9難度：0.8

  解析

• 6．已知圓C₁：x²+y²-x-y=0，圓C₂：x²+y²-mx-ny=0，若圓C₂平分圓C₁的周長，則m+n=（　　）

  A．1

  B．2

  C．4

  D． 1 2
  組卷：75引用：1難度：0.6

  解析

• 7．在數列{a_n}中，a₁=3，a_n=

  a

  n

  -

  1

  +

  2

  ，則（　　）

  A．數列{an}單調遞減	B．數列{an}單調遞增
  C．數列{an}先遞減后遞增	D．數列{an}先遞增后遞減
  組卷：41引用：1難度：0.9

  解析

四、解答題（共70分）

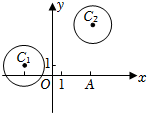• 21．如圖，在平面直角坐標系xOy中，已知圓C₁：（x+3）²+（y-1）²=4和圓C₂：（x-4）²+（y-5）²=4．
  （1）若直線l過點A（4，0），且被圓C₁截得的弦長為

  2

  3

  ，求直線l的方程；
  （2）設P為平面上的點，滿足：存在過點P的無窮多對互相垂直的直線l₁和l₂，它們分別與圓C₁和圓C₂相交，且直線l₁被圓C₁截得的弦長與直線l₂被圓C₂截得的弦長相等，試求所有滿足條件的點P的坐標．
  組卷：278引用：11難度：0.6

  解析

• 22．已知數列{a_n}（n∈N^*，1≤n≤50）滿足a₁=a,a_n+1-a_n=

  d , 1 ≤ n ≤ 15

  - d , 16 ≤ n ≤ 49

  ，其中d＞0，n∈N^*．
  （1）當a=1，d=2時，①求a₁₆，a₅₀；②求：|a₁|+|a₂|+|a₃|+?+|a₅₀|；
  （2）設集合M={b|b=a_i+a_j，i,j∈N^*，1≤i≤16，17≤j≤50}．是否存在實數a,d＞0，使1、6、

  55

  7

  都屬于M？若存在，請求出實數a和d；若不存在，請說明理由．
  組卷：31引用：2難度：0.4

  解析