2022-2023學年天津市重點校聯考高一(下)期末數學試卷
發布:2024/6/16 8:0:10
一、選擇題(本題共8小題,每小題4分,共32分)
-
1.已知(1+i)z=3+i,其中i為虛數單位,則|z|=( )
A. 5B.5 C.2 D. 2組卷:105引用:2難度:0.8 -
2.已知向量
=(-1,2),a=(1,1),則b在a上的投影向量為( )bA. 22B.(-1,2) C.( ,22)22D.( )12,12組卷:420引用:6難度:0.8 -
3.已知三條不同的直線l,m,n和兩個不同的平面α,β,下列四個命題中正確的為( )
A.若m∥α,n∥α,則m∥n B.若l∥m,m?α,則l∥α C.若l∥α,l∥β,則α∥β D.若l∥α,l⊥β,則α⊥β 組卷:916引用:11難度:0.6 -
4.已知△ABC中,角A,B,C所對的邊分別是a,b,c,若(a+b-c)(b+c+a)=3ab,且sinC=2sinBcosA,那么△ABC是( )
A.直角三角形 B.等腰三角形 C.等邊三角形 D.等腰直角三角形 組卷:131引用:2難度:0.7 -
5.在棱長為1的正方體ABCD-A1B1C1D1中,P為B1C1的中點,那么直線CP與B1D1所成角的余弦值是( )
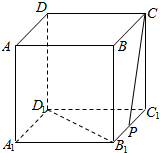
A. 32B. 1010C. 35D. 45組卷:642引用:7難度:0.9 -
6.盒中裝有形狀、大小完全相同的4個球,其中紅色球2個,黃色球2個.若從中隨機取出2個球,則所取出的2個球顏色相同的概率等于( )
A. 12B. 13C. 16D. 23組卷:217引用:1難度:0.8
三、解答題(本大題共5小題,共64分)
-
18.已知△ABC內角A,B,C的對邊分別為a,b,c,且3a+2b=3ccosB.
(1)求cosC的值;
(2)若,求△ABC的面積.c=31,a+b=6組卷:100引用:2難度:0.5 -
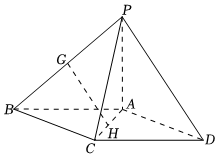 19.如圖,在四棱錐P-ABCD中,底面ABCD為平行四邊形,△PCD為等邊三角形,平面PAC⊥平面PCD,PA⊥CD,CD=4,AD=6.
19.如圖,在四棱錐P-ABCD中,底面ABCD為平行四邊形,△PCD為等邊三角形,平面PAC⊥平面PCD,PA⊥CD,CD=4,AD=6.
(1)設G,H分別為PB,AC的中點,求證:GH∥平面PAD;
(2)求證:PA⊥平面PCD;
(3)求直線AD與平面PAC所成角的正弦值.組卷:515引用:4難度:0.5


