2021-2022學年安徽省滁州市定遠縣民族中學高一（下）期末數學試卷

一、單選題（本大題共8小題，共40分）

• 1．設集合A={x|-1≤x≤3}，集合B={x|x≥a}，若A?B，則a的取值范圍為（　　）

  A．a≥3

  B．-1≤a≤3

  C．a≥-1

  D．a≤-1
  組卷：870引用：8難度：0.9

  解析

• 2．已知復數z滿足（1+

  3

  i）z=1+i,則復平面內與復數z對應的點在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：678引用：12難度：0.8

  解析

• 3．為比較甲，乙兩地某月14時的氣溫，隨機選取該月中的5天，將這5天中14時的氣溫數據（單位：℃）制成如圖所示的莖葉圖，考慮以下結論：
  ①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫；
  ②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫；
  ③甲地該月14時的氣溫的標準差小于乙地該月14時的氣溫的標準差；
  ④甲地該月14時的氣溫的標準差大于乙地該月14時的氣溫的標準差．
  其中根據莖葉圖能得到的統計結論的編號為（　　）

  A．①③

  B．①④

  C．②③

  D．②④
  組卷：1044引用：23難度：0.9

  解析

• 4．菱形ABCD的邊長為2，且∠DAB=60°，

  AB

  ?

  BC

  =（　　）

  A． 3

  B．-2

  C．2

  D． - 3
  組卷：44引用：2難度：0.9

  解析

• 5．已知函數y=Asin（ωx+φ）+m的最大值為4，最小值為0，兩個對稱軸間的最短距離為

  π

  2

  ，直線

  x

  =

  π

  6

  是其圖象的一條對稱軸，則符合條件的解析式是（　　）

  A． y = 4 sin （ 2 x + π 6 ）	B． y = - 2 sin （ 2 x + π 6 ） + 2
  C． y = - 2 sin （ x + π 3 ） + 2	D． y = 2 sin （ x + π 3 ） + 2
  組卷：255引用：14難度：0.7

  解析

• 6．函數

  y

  =

  2

  x

  x

  2

  +

  1

  的圖象大致為（　　）

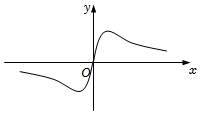
  A．	B．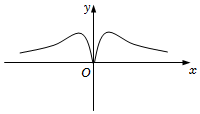
  C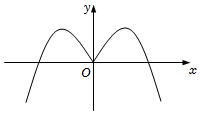．	D．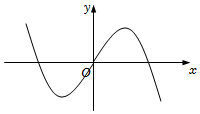
  組卷：412引用：11難度：0.7

  解析

• 7．若m,n是兩條不同的直線，α，β，γ是三個不同的平面，則下列命題中的真命題是（　　）

  A．若m?β，α⊥β，則m⊥α

  B．若m⊥β，m∥α，則α⊥β

  C．若α⊥γ，α⊥β，則β⊥γ

  D．若α∩γ=m,β∩γ=n,m∥n,則α∥β
  組卷：597引用：45難度：0.9

  解析

四、解答題（本大題共6小題，共70分）

• 21．已知定義域為R的函數

  f

  （

  x

  ）

  =

  3

  x

  -

  a

  3

  x

  +

  1

  是奇函數．
  （1）求a的值；
  （2）判斷f（x）的單調性，并證明；
  （3）若f（2m-m²）+f（2m+21）≤0，求實數m的取值范圍．
  組卷：416引用：6難度：0.5

  解析

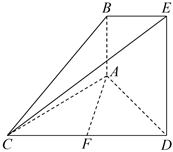• 22．如圖所示，已知AB⊥平面ACD，DE⊥平面ACD，△ACD為等邊三角形．AD=DE=2AB，F為CD的中點．
  （1）證明：AF∥平面BCE；
  （2）證明：平面BCE⊥平面CDE；
  （3）求直線AD和平面BCE所成的角的正弦值．
  組卷：158引用：3難度：0.6

  解析