當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省臨沂市蘭山區高一（下）期中數學試卷

發布：2024/6/5 8:0:7

一、單選題：本題共8小題，每題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知z=2+i,其中i為虛數單位，則在復平面內z的共軛復數對應的點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：45引用：4難度：0.8
解析
2．下列化簡不正確的是（　　）
A．cos82°sin52°+sin82°cos128°=-
1
2
B．sin15°sin30°sin75°=
1
8
C．cos²15°-sin²15°=
3
2
D．
tan
48
°
+
tan
72
°
1
-
tan
48
°
tan
72
°
=
3
組卷：261引用：7難度：0.6
解析
3．已知
tanα
=
1
2
，
tanβ
=
-
1
7
，則tan（2α+β）的值為（　　）
A．
-
3
4
B．
-
31
17
C．1 D．
31
17
組卷：170引用：1難度：0.8
解析
4．已知△ABC的外接圓圓心為O，且
2
AO
=
AB
+
AC
，
|
OA
|
=
|
AB
|
，則向量
CA
在向量
BC
上的投影向量為（　　）
A．
1
4
BC
B．
3
4
BC
C．
-
1
4
BC
D．
-
3
4
BC
組卷：125引用：6難度：0.6
解析
5．蜜蜂的巢房是令人驚嘆的神奇天然建筑物．巢房是嚴格的六角柱狀體，它的一端是平整的六角形開口，另一端是封閉的六角菱形的底，由三個相同的菱形組成．巢中被封蓋的是自然成熟的蜂蜜．如圖是一個蜂巢的正六邊形開口ABCDEF，下列說法正確的是（　　）
A．
AC
-
AE
=
BF
B．
AC
+
AE
=
1
2
AD
C．
AD
?
AB
=
AD
?
DE
D．
AD
=
2
（
AB
+
AF
）
組卷：46引用：3難度：0.6
解析
6．若平面向量
a
，
b
的夾角為60°，且|
a
|=2|
b
|，則（　　）
A．
a
⊥（
b
+
a
） B．
b
⊥（
b
-
a
） C．
b
⊥（
b
+
a
） D．
a
⊥（
b
-
a
）
組卷：75引用：5難度：0.9
解析
7．一艘海輪從A處出發，以每小時40海里的速度沿南偏東40°的方向直線航行，2小時后到達B處，在C處有一座燈塔，海輪在A處觀察燈塔，其方向是南偏東70°，在B處觀察燈塔，其方向是北偏東65°，那么B，C兩點間的距離是（　　）
A．
40
2
海里 B．
40
3
海里 C．
80
3
海里 D．
80
2
海里
組卷：314引用：12難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明或驗算步驟．

21．設函數
f
（
x
）
=
sin
（
2
x
-
π
6
）
+
2
co
s
2
x
-
1
．
（1）當
x
∈
[
0
，
π
2
]
時，求函數f（x）的值域；
（2）△ABC的內角A，B，C所對的邊分別為a,b,c,且
f
（
A
）
=
1
2
，
2
a
=
3
b
，
c
=
1
+
3
，求△ABC的面積．
組卷：48引用：2難度：0.5
解析
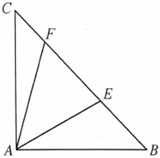22．如圖，某小區有一塊空地△ABC，其中AB=50，AC=50，∠BAC=90°，小區物業擬在中間挖一個小池塘△AEF，E，F在邊BC上（E，F不與B，C重合，且E在B，F之間），且
∠
EAF
=
π
4
．
（1）若
BE
=
10
2
，求EF的值；
（2）為節省投入資金，小池塘△AEF的面積需要盡可能的小．設∠EAB=θ，試確定θ的值，使得△AEF的面積取得最小值，并求出△AEF面積的最小值．
組卷：614引用：9難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． AC - AE = BF	B． AC + AE = 1 2 AD
C． AD ? AB = AD ? DE	D． AD = 2 （ AB + AF ）

2022-2023學年山東省臨沂市蘭山區高一（下）期中數學試卷

一、單選題：本題共8小題，每題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知z=2+i,其中i為虛數單位，則在復平面內z的共軛復數對應的點位于（ ）

2．下列化簡不正確的是（ ）

3．已知tanα=12，tanβ=-17，則tan（2α+β）的值為（ ）

4．已知△ABC的外接圓圓心為O，且2AO=AB+AC，|OA|=|AB|，則向量CA在向量BC上的投影向量為（ ）

6．若平面向量a，b的夾角為60°，且|a|=2|b|，則（ ）

7．一艘海輪從A處出發，以每小時40海里的速度沿南偏東40°的方向直線航行，2小時后到達B處，在C處有一座燈塔，海輪在A處觀察燈塔，其方向是南偏東70°，在B處觀察燈塔，其方向是北偏東65°，那么B，C兩點間的距離是（ ）

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明或驗算步驟．

21．設函數f（x）=sin（2x-π6）+2cos2x-1．（1）當x∈[0，π2]時，求函數f（x）的值域；（2）△ABC的內角A，B，C所對的邊分別為a,b,c,且f（A）=12，2a=3b，c=1+3，求△ABC的面積．

1．已知z=2+i,其中i為虛數單位，則在復平面內z的共軛復數對應的點位于（　　）

2．下列化簡不正確的是（　　）

3．已知
tanα
=
1
2
，
tanβ
=
-
1
7
，則tan（2α+β）的值為（　　）

4．已知△ABC的外接圓圓心為O，且
2
AO
=
AB
+
AC
，
|
OA
|
=
|
AB
|
，則向量
CA
在向量
BC
上的投影向量為（　　）

6．若平面向量
a
，
b
的夾角為60°，且|
a
|=2|
b
|，則（　　）

7．一艘海輪從A處出發，以每小時40海里的速度沿南偏東40°的方向直線航行，2小時后到達B處，在C處有一座燈塔，海輪在A處觀察燈塔，其方向是南偏東70°，在B處觀察燈塔，其方向是北偏東65°，那么B，C兩點間的距離是（　　）

21．設函數
f
（
x
）
=
sin
（
2
x
-
π
6
）
+
2
co
s
2
x
-
1
．
（1）當
x
∈
[
0
，
π
2
]
時，求函數f（x）的值域；
（2）△ABC的內角A，B，C所對的邊分別為a,b,c,且
f
（
A
）
=
1
2
，
2
a
=
3
b
，
c
=
1
+
3
，求△ABC的面積．