2023-2024學年湖北省武漢市華中師大一附中高二(上)月考數學試卷(9月份)
發布:2024/9/6 15:0:11
一、單選題:本大題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一個選項符合題目要求.
-
1.已知直線a,b的方向向量分別為
,a=(1,0,-1),且直線a,b均平行于平面α,平面α的單位法向量為( )b=(1,-1,0)A. (33,33,33)B. (-33,-33,-33)C.(1,1,1) D. 或(33,33,33)(-33,-33,-33)組卷:51引用:4難度:0.7 -
2.已知點A(2,3,5),B(2,-1,-1)是空間直角坐標系O-xyz中的兩點,點B關于xOy平面對稱的點為B′,線段AB′的中點與點B的距離為( )
A. 25B. 22C. 32D. 17組卷:19引用:2難度:0.7 -
3.已知
是空間的一組單位正交基底,若向量{a,b,c}在基底p下用有序實數組表示為(3,2,1),則與向量{a,b,c}同向的單位向量在基底p下用有序實數組表示為( ){a,b+c,b-c}A. (34623,34646,4646)B. (31414,147,1414)C. (31414,31428,1428)D. (-31414,-31428,-1428)組卷:45引用:2難度:0.6 -
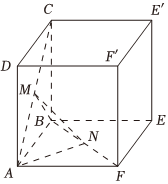 4.如圖,在正方體ABEFDCE′F′中,M,N分別為AC,BF的中點,則平面MNA與平面MNB的夾角的余弦值為( )
4.如圖,在正方體ABEFDCE′F′中,M,N分別為AC,BF的中點,則平面MNA與平面MNB的夾角的余弦值為( )A.- 13B. 13C.- 223D. 223組卷:123引用:4難度:0.5 -
5.若
,OA=(0,0,1),OB=(2,-1,2),則三棱錐O-ABC的體積為( )OC=(1,2,3)A. 56B. 52C. 53D. 5組卷:25引用:2難度:0.6 -
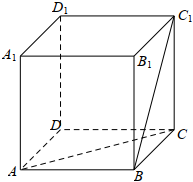 6.如圖,已知正方體ABCD-A1B1C1D1的棱長為2,點P為線段BC1上的動點,則點P到直線AC的距離的最小值為( )
6.如圖,已知正方體ABCD-A1B1C1D1的棱長為2,點P為線段BC1上的動點,則點P到直線AC的距離的最小值為( )A.1 B. 22C. 233D. 64組卷:362引用:5難度:0.6 -
7.兩條異面直線a,b所成的角為60°,在直線a,b上分別取點A,E和點B,F,使AB⊥a,且AB⊥b.已知AE=6,BF=8,EF=14,則線段AB的長為( )
A.20或12 B.12或 43C. 或4383D. 或2083組卷:143引用:5難度:0.6
四、解答題(本大題共6小題,共70分)
-
 21.如圖,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,E,F分別是棱AA1,BB1上的點,.A1E=BF=13AA1
21.如圖,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,E,F分別是棱AA1,BB1上的點,.A1E=BF=13AA1
(1)證明:平面CEF⊥平面ACC1A1;
(2)求直線AC1與平面CFC1夾角余弦值.組卷:41引用:2難度:0.5 -
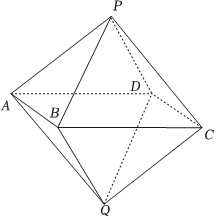 22.如圖,在八面體PABCDQ中,四邊形ABCD是邊長為2的正方形,平面PAD∥平面QBC,二面角P-AB-C與二面角Q-CD-A的大小都是30°,,PD⊥AB.AP=CQ=3
22.如圖,在八面體PABCDQ中,四邊形ABCD是邊長為2的正方形,平面PAD∥平面QBC,二面角P-AB-C與二面角Q-CD-A的大小都是30°,,PD⊥AB.AP=CQ=3
(1)證明:平面PCD∥平面QAB;
(2)設G為△QBC的重心,是否在棱PA上存在點S,使得SG與平面ABCD所成角的正弦值為,若存在,求S到平面ABCD的距離,若不存在,說明理由.3020組卷:143引用:6難度:0.5


