2022-2023學(xué)年山東省濟(jì)南市萊蕪區(qū)魯西中學(xué)八年級（上）第一次作業(yè)檢查數(shù)學(xué)試卷（五四學(xué)制）

一、選擇題

• 1．下列能組成三角形的線段是（　　）

  A．3cm,2cm,6cm	B．4cm,7cm,5cm
  C．2cm,4cm,6cm	D．3cm,6cm,9cm
  組卷：86引用：4難度：0.6

  解析

• 2．以下列長度的三條線段為邊，能構(gòu)成三角形的是（　　）

  A．7，8，15

  B．15，20，4

  C．7，6，18

  D．6，7，5
  組卷：520引用：10難度：0.6

  解析

• 3．如圖，已知∠AOB，求作：∠DEF，使∠DEF=∠AOB
  作法：（1）以點(diǎn)O為圓心，任意長為半徑畫，分別交OA，OB于點(diǎn)P，Q；
  （2）作射線EG，并以點(diǎn)E為圓心，OP長為半徑畫弧交EG于點(diǎn)D；
  （3）以點(diǎn)D為圓心，PQ長為半徑畫弧交第（2）步中所畫弧于點(diǎn)F；
  （4）作射線EF，∠DEF即為所求作的角．
  
  根據(jù)以上作法，可以判斷出△OPQ≌△EDF的方法是（　　）

  A．SAS

  B．SSS

  C．ASA

  D．AAS
  組卷：511引用：5難度：0.9

  解析

• 4．如圖，△ABC≌△DCB，若AC=7，BE=5，則DE的長為（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：5527引用：79難度：0.9

  解析

• 5．如圖，有一池塘，要測池塘兩端A，B間的距離，可先在平地上取一個(gè)不經(jīng)過池塘可以直接到達(dá)點(diǎn)A和B的點(diǎn)C，連接AC并延長至D，使CD=CA，連接BC并延長至E，使CE=CB，連接ED．若量出DE=58米，則A，B間的距離即可求．依據(jù)是（　　）

  A．SAS

  B．SSS

  C．AAS

  D．ASA
  組卷：2112引用：11難度：0.8

  解析

• 6．等腰三角形中，有一個(gè)角是40°，它的一條腰上的高與底邊的夾角是（　　）

  A．20°

  B．50°

  C．25°或40°

  D．20°或50°
  組卷：1351引用：8難度：0.5

  解析

• 7．如圖，∠BAC=∠ACD=90°，∠ABC=∠ADC，CE⊥AD，且BE平分∠ABC，則下列結(jié)論：①AD=CB；②∠ACE=∠ABC；③∠ECD+∠EBC=∠BEC；④∠CEF=∠CFE；其中正確的是（　　）

  A．①②

  B．①③④

  C．①②④

  D．①②③④
  組卷：1180引用：3難度：0.7

  解析

• 8．在實(shí)數(shù)-1.414，

  2

  ，π，3.

  ?

  1

  ?

  4

  ，2+

  3

  ，3.212212221…，3.14中，無理數(shù)的個(gè)數(shù)是（　　）個(gè)．

  A．1

  B．2

  C．3

  D．4
  組卷：939引用：14難度：0.7

  解析

• 9．下列計(jì)算正確的是（　　）

  A． （ - 3 ） 2 =-3

  B．- 0 . 36 =-0.6

  C． 36 =±6

  D． 3 - 5 = 3 5
  組卷：532引用：17難度：0.8

  解析

三、解答題

• 26．如圖1，點(diǎn)B是線段AD上一點(diǎn)，△ABC和△BDE分別是等邊三角形，連接AE和CD，交于點(diǎn)M．
  （1）求證：AE=CD．
  （2）求∠AMC的度數(shù)．
  （3）如圖2，點(diǎn)P，Q分別是AE，CD的中點(diǎn)，試判斷△PBQ的形狀，并說明理由．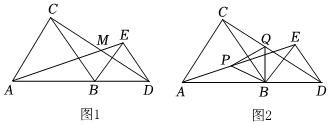
  
  組卷：135引用：4難度：0.4

  解析

• 27．在△ABC中，AB=AC，∠BAC=120°，以CA為邊在∠ACB的另一側(cè)作∠ACM=∠ACB，點(diǎn)D為射線CM上任意一點(diǎn)，在射線CM上載取CE=BD，連接AD、AE．
  （1）如圖1，當(dāng)點(diǎn)D落在線段BC的延長線上時(shí)，求證：△ABD≌△ACE；
  （2）在（1）的條件下，求出∠ADE的度數(shù)；
  （3）如圖2，當(dāng)點(diǎn)D落在線段BC（不含端點(diǎn)）上時(shí)，作AH⊥BC，垂足為H，作AG⊥EC，垂足為G，連接HG，判斷△GHC的形狀，并說明理由．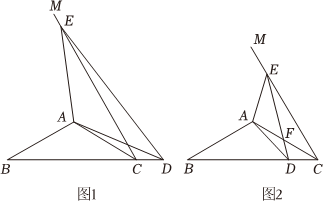
  
  組卷：755引用：3難度：0.3

  解析