當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省江門市棠下中學高二（上）月考數學試卷（10月份）

發布：2024/8/12 21:0:2

1．已知
a
=
（
2
，-
1
，
3
）
，
b
=
（
-
2
，
x
,
1
）
，若
a
⊥
b
，則x=（　　）
A．-1 B．1 C．0 D．2
組卷：41引用：3難度：0.8
解析
2．若A（-1，-2），B（4，8），C（5，x），且A，B，C三點共線，則x=（　　）
A．-2 B．5 C．10 D．12
組卷：393引用：10難度：0.8
解析
3．已知點A（-3，1，-4），B（7，1，0），則線段AB的中點M關于平面Oyz對稱的點的坐標為（　　）
A．（-2，1，-2） B．（2，1，-2） C．（2，-1，-2） D．（2，1，2）
組卷：100引用：9難度：0.7
解析
4．在棱長為1的正方體ABCD-A₁B₁C₁D₁中，設
AB
=
a
，
AD
=
b
，
A
A
1
=
c
，則
a
?
（
b
+
c
）
的值為（　　）
A．1 B．0 C．-1 D．-2
組卷：552引用：14難度：0.8
解析
5．在四面體OABC中，空間的一點M滿足
OM
=
1
4
OA
+
1
6
OB
+
λ
OC
，若
MA
，
MB
，
MC
共面，則λ=（　　）
A．
1
2
B．
1
3
C．
5
12
D．
7
12
組卷：1080引用：7難度：0.8
解析
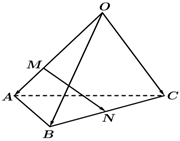6．如圖所示，在四面體O-ABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，點M在OA上，且
OM
=2
MA
，N為BC的中點，則
MN
=（　　）
A．
1
2
a
-
2
3
b
+
1
2
c
B．-
2
3
a
+
1
2
b
+
1
2
c
C．
1
2
a
+
1
2
b
-
2
3
c
D．
2
3
a
+
2
3
b
-
1
2
c
組卷：1254引用：41難度：0.9
解析

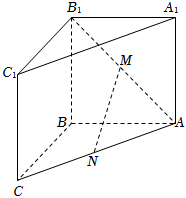19．如圖，在三棱柱ABC-A₁B₁C₁中，側面ABB₁A₁，BCC₁B₁都是正方形，∠ABC為直角，AB=2，M，N分別為AB₁，AC的中點．
（I）求證：MN∥平面BCC₁B₁；
（Ⅱ）求直線AB與平面AMN所成角的正弦值．
組卷：209引用：5難度：0.6
解析
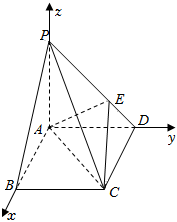20．如圖所示，四棱錐P-ABCD的底面是邊長為1的正方形，PA⊥CD，PA=1，PD=
2
，E為PD上一點，PE=2ED．
①求證：PA⊥平面ABCD；
②在側棱PC上是否存在一點F，使得BF∥平面AEC？若存在，指出F點的位置，并證明；若不存在，說明理由．
組卷：141引用：7難度：0.6
解析

A． 1 2 a - 2 3 b + 1 2 c	B．- 2 3 a + 1 2 b + 1 2 c
C． 1 2 a + 1 2 b - 2 3 c	D． 2 3 a + 2 3 b - 1 2 c

1．已知a=（2，-1，3），b=（-2，x,1），若a⊥b，則x=（ ）