2022-2023學年山東省煙臺市萊州一中高二（下）第二次質檢數學試卷（6月份）

一、單選題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．函數

  f

  （

  x

  ）

  =

  2 x ， x ≥ 0

  f （ x + 3 ） ， x ＜ 0

  ，則f（-8）=（　　）

  A．4

  B．2

  C．8

  D．6
  組卷：9引用：5難度：0.8

  解析

• 2．設函數 f（x）=x²+ax,且

  lim

  △

  x

  →

  0

  f

  （

  1

  +

  △

  x

  ）

  -

  f

  （

  1

  ）

  △

  x

  =

  1

  ，則a=（　　）

  A． - 2 3

  B． - 3 2

  C．1

  D．-1
  組卷：987引用：7難度：0.8

  解析

• 3．已知函數f（x-1）=x²-2x,且f（a）=3，則實數a的值等于（　　）

  A． 2

  B． ± 2

  C．2

  D．±2
  組卷：260引用：4難度：0.9

  解析

• 4．下列求導運算正確的是（　　）

  A．（lnx+ 3 x ）′= 1 x + 3 x 2

  B．（x2ex）′=2xex

  C．（3xcos2x）′=3x（ln3?cos2x-2sin2x）

  D． （ ln 1 2 + lo g 2 x ） ′ = 2 + 1 xln 2
  組卷：232引用：5難度：0.7

  解析

• 5．“0＜a＜4”是“函數f（x）=

  1

  a

  x

  2

  -

  ax

  +

  1

  的定義域為R”的（　　）

  A．必要不充分條件	B．充分不必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：97引用：6難度：0.8

  解析

• 6．若直線y=x與曲線y=e^2x+m（m∈R，e為自然對數的底數）相切，則m=（　　）

  A．-2

  B．-1-ln2

  C．-ln2

  D．2
  組卷：212引用：3難度：0.7

  解析

• 7．已知函數f（x）與其導函數f'（x）的圖象如圖所示，則函數g（x）=

  f

  （

  x

  ）

  e

  x

  的單調遞減區間為（　　）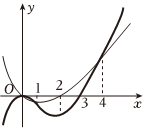

  A．（0，1）和（4，+∞）	B．（0，2）
  C．（-∞，0）和（1，4）	D．（0，3）
  組卷：288引用：2難度：0.4

  解析

四、解答題（本題共6小題，共70分，其中第17題10分，其它每題12分，解答應寫出文字說明、證明過程或演算步驟．）

• 21．已知函數

  f

  （

  x

  ）

  =

  e x - 1 ， x ≥ 0

  1 2 a x 2 - ax , x ＜ 0

  ，其中a≠0．
  （1）若f（x）在R上單調遞增，求實數a的取值范圍；
  （2）對?x₂＞0，?x₁，使得f（x₁）=f（x₂），且x₁+x₂＜0，求實數a的取值范圍．
  組卷：196引用：4難度：0.3

  解析

• 22．已知函數f（x）=lnx-x+2sinx.
  （1）證明：f（x）在區間（0，

  π

  2

  ）存在唯一的極值點；
  （2）試討論f（x）的零點個數．
  組卷：154引用：2難度：0.4

  解析