2022-2023學年上海外國語大學附屬大境中學高二（上）期中數學試卷

一、填空題（本大題共12題，1-6每題4分，7-12每題5分，共54分）

• 1．已知球的體積為36π，則該球大圓的面積等于

  ．
  組卷：107引用：7難度：0.7

  解析

• 2．已知正四棱柱ABCD-A₁B₁C₁D₁的底面邊長為2，高為3．則異面直線AA₁，BD₁所成角的大小是

  ．
  組卷：13引用：1難度：0.7

  解析

• 3．已知正六棱錐底面邊長為a,體積為

  3

  2

  a³，則側棱與底面所成的角為

   

  ．
  組卷：146難度：0.5

  解析

• 4．棱長為a的正方體ABCD-A₁B₁C₁D₁的頂點A到截面B₁CD的距離等于

  ．
  組卷：106引用：5難度：0.7

  解析

• 5．已知一個正方體的所有頂點在一個球面上，若這個正方體的表面積為18，則這個球的體積為

  ．
  組卷：5608引用：18難度：0.5

  解析

• 6．已知△ABC，點P是平面ABC外一點，點O是點P在平面ABC上的射影，且點O在△ABC內．若點P到△ABC的三邊所在直線的距離相等，則點O一定是△ABC的

  心．
  組卷：24引用：1難度：0.7

  解析

• 7．我國南北朝時期的數學家祖暅提出了一個原理“冪勢既同，則積不容異“，現有某幾何體和一個圓錐滿足祖暅原理的條件，若該圓錐的側面展開圖是一個半徑為2的半圓，則該幾何體的體積為

  ．
  組卷：44引用：1難度：0.7

  解析

三、解答題（本大題共5題，8+8+10+12+12，共50分）

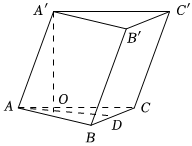• 20．已知斜三棱柱ABC-A'B'C'的底面是正三角形，側棱AA'⊥BC，并且與底面所成角是60°．設側棱長為l.
  （1）求此三棱柱的高；
  （2）求證：側面BB'C'C是矩形；
  （3）求證：A'在平面ABC上的射影O在∠BAC的平分線上．
  組卷：78引用：2難度：0.6

  解析

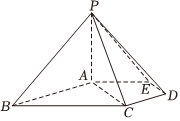• 21．如圖，在五棱錐P-ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，∠ABC=45°，AB=2

  2

  ，BC=2AE=4，三角形PAB是等腰三角形．
  （1）求證：平面PCD⊥平面PAC；
  （2）求直線PB與平面PCD所成角的大?。?/h2>
  組卷：56引用：6難度：0.5

  解析