2022-2023學年湖南省湘潭市高三（上）入學數(shù)學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={x∈R|x²-x=0}，B={x∈R|x²+x≠0}，則A∩B=（　　）

  A．{1}

  B．{-1}

  C．{0，1}

  D．{-1，0，1}
  組卷：82引用：3難度：0.7

  解析

• 2．復(fù)數(shù)

  （

  1

  -

  i

  1

  +

  i

  ）

  5

  =（　　）

  A．-1

  B．1

  C．-i

  D．i
  組卷：23引用：1難度：0.8

  解析

• 3．若函數(shù)f（x）=sin2x的圖象由函數(shù)g（x）=cos2x的圖象經(jīng)過以下變換得到的，則該變換為（　　）

  A．向左平移 π 2 個單位長度	B．向左平移 π 4 個單位長度
  C．向右平移 π 2 個單位長度	D．向右平移 π 4 個單位長度
  組卷：141引用：1難度：0.7

  解析

• 4．已知直三棱柱ABC-A₁B₁C₁的側(cè)棱和底面邊長均為1，M，N分別是棱BC，A₁B₁上的點，且CM=2B₁N=λ，當MN∥平面AA₁C₁C時，λ的值為（　　）

  A． 3 4

  B． 2 3

  C． 1 2

  D． 1 3
  組卷：164引用：1難度：0.9

  解析

• 5．設(shè)某芯片制造廠有甲、乙兩條生產(chǎn)線均生產(chǎn)5nm規(guī)格的芯片，現(xiàn)有20塊該規(guī)格的芯片，其中甲、乙生產(chǎn)的芯片分別為12塊，8塊，且乙生產(chǎn)該芯片的次品率為

  1

  20

  ，現(xiàn)從這20塊芯片中任取一塊芯片，若取得芯片的次品率為0.08，則甲廠生產(chǎn)該芯片的次品率為（　　）

  A． 1 5

  B． 1 10

  C． 1 15

  D． 1 20
  組卷：63引用：7難度：0.7

  解析

• 6．牛頓迭代法亦稱切線法，它是求函數(shù)零點近似解的另一種方法．若定義x_k（k∈N）是函數(shù)零點近似解的初始值，過點P_k（x_k，f（x_k））的切線為y=f'（x_k）（x-x_k）+f（x_k），切線與x軸交點的橫坐標為x_k+1，即為函數(shù)零點近似解的下一個初始值，以此類推，滿足精度的初始值即為函數(shù)零點近似解．設(shè)函數(shù)f（x）=x²-5，滿足x₀=1．應(yīng)用上述方法，則x₃=（　　）

  A．3

  B． 7 3

  C． 47 21

  D． 51 21
  組卷：63引用：1難度：0.6

  解析

• 7．在四邊形ABCD中，G為△BCD的重心，AG=2，點O在線段AG上，則

  OA

  ?

  （

  OB

  +

  OC

  +

  OD

  ）

  的最小值為（　　）

  A．-3

  B．-2

  C．-1

  D．0
  組卷：97引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出必要的文字說明、證明過程及演算步驟．

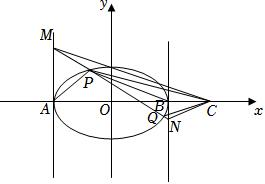• 21．如圖，已知A，B兩點的坐標分別為（-2，0），（2，0），直線AP，BP的交點為P，且它們的斜率之積為

  -

  1

  4

  ．
  （1）求點P的軌跡E的方程；
  （2）設(shè)點C為x軸上（不同于A，B）一定點，若過點P的動直線與E的交點為Q，直線PQ與直線x=-2和直線x=2分別交于M，N兩點，求證：∠ACM=∠ACN的充要條件為∠ACP=∠ACQ．
  組卷：39引用：1難度：0.4

  解析

• 22．已知f（x）=e^1-x+（a+1）lnx.
  （1）若f（x）在定義域上單調(diào)遞增，求a的取值范圍；
  （2）設(shè)函數(shù)g（x）=f（x）-ax,其中a≥

  1

  e

  ，若g（x）存在兩個不同的零點x₁，x₂．
  ①求a的取值范圍；
  ②證明：x₁+x₂＞2．
  組卷：65引用：1難度：0.2

  解析