2022-2023學(xué)年陜西省西安市臨潼區(qū)高二（下）月考數(shù)學(xué)試卷（文科）（5月份）

一、選擇題（本大題共12小題，每小題4分，共48分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)符合題目要求）

• 1．為了解某地區(qū)中小學(xué)生的視力情況，擬從該地區(qū)的中小學(xué)生中抽取部分學(xué)生進(jìn)行調(diào)查，事先已經(jīng)了解到該地區(qū)小學(xué)、初中、高中三個(gè)學(xué)段學(xué)生的視力情況有較大差異，而男女生視力情況差異不大．在下面的抽樣方法中，最合理的抽樣方法是（　　）

  A．簡(jiǎn)單的隨機(jī)抽樣	B．按性別分層抽樣
  C．按學(xué)段分層抽樣	D．系統(tǒng)抽樣
  組卷：4164引用：68難度：0.9

  解析

• 2．設(shè)a,b,c,d是非零實(shí)數(shù)，則“ad=bc”是“a,b,c,d成等比數(shù)列”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：3365引用：19難度：0.9

  解析

• 3．已知函數(shù)

  f

  （

  x

  ）

  =

  2 x + 1 - 1 ， x ＜ 1

  f （ x - 1 ） ， x ≥ 1

  ，則f（log₂3）=（　　）

  A．3

  B．2

  C．-3

  D．-2
  組卷：28引用：3難度：0.6

  解析

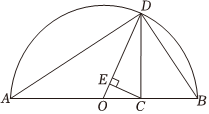• 4．《幾何原本》中的幾何代數(shù)法是以幾何方法研究代數(shù)問(wèn)題，這種方法是數(shù)學(xué)家處理問(wèn)題的重要依據(jù)，很多代數(shù)公理、定理都可以根據(jù)這一原理實(shí)現(xiàn)證明，也稱(chēng)為“無(wú)字證明”．如圖，AB是圓O的直徑，點(diǎn)O為圓心，點(diǎn)C是線段AB上的一點(diǎn)，且AC=m,BC=n.過(guò)點(diǎn)C作垂直于AB的半弦DC，連接DA，DB，DO，過(guò)點(diǎn)C作CE垂直DO于點(diǎn)E，則根據(jù)該圖形我們可以完成的無(wú)字證明有（　　）
  ①m²+n²≥2mn（m＞0，n＞0）
  ②

  mn

  ≤

  m

  +

  n

  2

  （

  m

  ＞

  0

  ，

  n

  ＞

  0

  ）

  
  ③

  m

  2

  +

  n

  2

  2

  ≥

  （

  m

  +

  n

  2

  ）

  2

  （

  m

  ＞

  0

  ，

  n

  ＞

  0

  ）

  
  ④

  mn

  ≥

  2

  1

  m

  +

  1

  n

  （

  m

  ＞

  0

  ，

  n

  ＞

  0

  ）

  A．①②

  B．①③

  C．②③

  D．②④
  組卷：151引用：1難度：0.6

  解析

• 5．已知點(diǎn)（1，4）在拋物線y=ax²上，則拋物線的焦點(diǎn)坐標(biāo)為（　　）

  A．（1，0）

  B．（0，1）

  C． （ 0 ， 1 16 ）

  D． （ 1 16 ， 0 ）
  組卷：117引用：1難度：0.8

  解析

• 6．向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  b

  =

  （

  0

  ，

  1

  ）

  ，

  c

  =

  a

  +

  k

  b

  ，若

  a

  ⊥

  c

  ，則k=（　　）

  A．0

  B．-2

  C．8

  D．-10
  組卷：81引用：5難度：0.8

  解析

• 7．已知集合

  A

  =

  {

  x

  |

  |

  x

  -

  1

  i

  |

  ≤

  2

  （

  i

  為虛數(shù)單位

  ）

  }

  ，集合

  B

  =

  {

  x

  |

  x

  2

  -

  1

  x

  ≤

  0

  }

  ，則A∩B=（　　）

  A．{x|0＜x≤1或x=-1}	B．{x|0≤x≤1}
  C．{x|0＜x＜1}	D．{x|0≤x＜1}
  組卷：14引用：1難度：0.7

  解析

三.解答題（本大題共5小題，共計(jì)56分.解答題應(yīng)寫(xiě)出必要的文字說(shuō)明，證明過(guò)程或演算步驟）

• 20．設(shè)f（x）=e^x（ax²+x+1），且曲線y=f（x）在x=1處的切線與x軸平行．
  （1）求a的值，并討論f（x）的單調(diào)性；
  （2）證明：當(dāng)

  θ

  ∈

  [

  0

  ，

  π

  2

  ]

  時(shí)

  ，

  |

  f

  （

  cosθ

  ）

  -

  f

  （

  sinθ

  ）

  |

  ＜

  2

  ．
  組卷：706引用：9難度：0.5

  解析

• 21．已知點(diǎn)E（

  2

  ，0），F(xiàn)（

  2

  2

  ，0），點(diǎn)A滿足|AE|=

  2

  |AF|，點(diǎn)A的軌跡為曲線C．
  （Ⅰ）求曲線C的方程；
  （Ⅱ）若直線l：y=kx+m與雙曲線：

  x

  2

  4

  -

  y

  2

  9

  =1交于M，N兩點(diǎn)，且∠MON=

  π

  2

  （O為坐標(biāo)原點(diǎn)），求點(diǎn)A到直線l距離的取值范圍．
  組卷：213引用：3難度：0.6

  解析