2022-2023學年安徽省滁州市定遠中學高一（下）段考數學試卷（6月份）（三）

一、單選題（本大題共8小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．已知某校高三年級共1200人，其中實驗班200人，為了解學生們的學習狀況，高三年級組織了一次全員的數學測驗，現將全部數學試卷用分層抽樣的方法抽取60份進行研究，則樣本中實驗班的試卷份數為（　　）

  A．5

  B．10

  C．20

  D．25
  組卷：56引用：3難度：0.8

  解析

• 2．若復數z滿足（1+i）z=|1+i|，則z的虛部為（　　）

  A． - 2 i

  B． - 2

  C． - 2 2 i

  D． - 2 2
  組卷：80引用：12難度：0.9

  解析

• 3．已知α，β是兩個不同的平面，m為平面α內的一條直線，下列說法正確的是（　　）

  A．若m∥β，則α∥β	B．若l?β，m∥l,則m∥β
  C．若α⊥β，則m⊥β	D．若m⊥β，則α⊥β
  組卷：80引用：5難度：0.5

  解析

• 4．已知向量

  a

  ，

  b

  滿足

  |

  b

  |

  =

  1

  ，

  a

  ⊥

  b

  ，則

  a

  -

  2

  b

  在

  b

  方向上的投影向量為（　　）

  A．2

  B． 2 a

  C． - 2 b

  D．-2
  組卷：377引用：8難度：0.9

  解析

• 5．已知m、n是兩條不同的直線，α、β、γ是三個不同的平面．下列說法中錯誤的是（　　）

  A．若m∥α，m?β，α∩β=n,則m∥n

  B．若m∥n,m∥α，則n∥α

  C．若α∩β=n,α⊥γ，β⊥γ，則n⊥γ

  D．若m⊥α，m⊥β，α∥γ，則β∥γ
  組卷：191引用：3難度：0.4

  解析

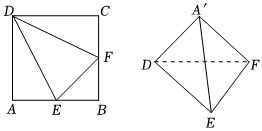• 6．在邊長為2的正方形ABCD中，E是AB的中點，點F是BC的中點，將△AED，△BEF，△DCF分別沿DE，EF，DF折起，使A，B，C三點重合于點A′，則A′到平面EFD的距離為（　　）

  A．1

  B． 2 3

  C． 4 3

  D．2
  組卷：119引用：5難度：0.5

  解析

• 7．已知平面向量

  a

  ，

  b

  ，

  c

  滿足

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  且對?t∈R，有

  |

  b

  +

  t

  a

  |

  ≥

  |

  b

  -

  a

  |

  恒成立，則

  2

  a

  -

  b

  與

  b

  的夾角為（　　）

  A． 2 π 3

  B． π 2

  C． π 3

  D． π 6
  組卷：290引用：4難度：0.5

  解析

四、解答題（本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

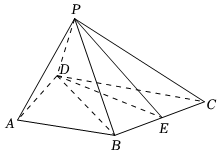• 21．如圖，在四棱錐P-ABCD中，PD=2，AB=3，AD=

  3

  ，∠DAB=90°，△BCD為正三角形，E是BC的中點，DE=PE，PD⊥BC．
  （1）求證：平面PDE⊥平面PBC；
  （2）求二面角P-BC-D的余弦值；
  （3）求四棱錐P-ABCD的體積．
  組卷：392引用：3難度：0.4

  解析

• 22．在△ABC中，三個內角A、B、C所對的邊分別為a、b、c,請在①（2c-a）cosB=bcosA；②a²+c²-b²=

  4

  3

  3

  S_△ABC；③2bsin（A+

  π

  6

  ）=a+c,這三個條件中任意選擇一個，完成下列問題：
  （1）若3a+b=2c,求cosC；
  （2）若b=2，且

  1

  sin

  A

  +

  1

  sin

  C

  =

  4

  3

  3

  ，求△ABC的面積．
  組卷：104引用：2難度：0.5

  解析