2022年陜西省西安市臨潼區高考數學二模試卷（理科）

一、選擇題（本題共12小題，每小題5分，計60分在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設A={x|lgx＞1}，B={x|x²-x-2＜0}，則?_RA∩B=（　　）

  A．{x|-1＜x≤1}

  B．{x|x＞-1}

  C．{x|-1＜x＜1}

  D．{x|-1＜x＜2}
  組卷：75引用：2難度：0.8

  解析

• 2．2022年1月，中科大潘建偉團隊和南科大范靖云團隊發表學術報告，分別獨立通過實驗，驗證了虛數i在量子力學中的必要性，再次說明了虛數i的重要性．對于方程x³+1=0，它的兩個虛數根分別為（　　）

  A． 1 ± 3 i 2

  B． - 1 ± 3 i 2

  C． ± 1 + 3 i 2

  D． ± 1 - 3 i 2
  組卷：36引用：2難度：0.8

  解析

• 3．以邊長為2的正方形一邊所在直線為軸旋轉一周，所得到的幾何體的體積為（　　）

  A．2π

  B．8π

  C． 2 π 3

  D． 8 π 3
  組卷：364引用：4難度：0.8

  解析

• 4．下列說法正確的是（　　）

  A．“A與B是互斥事件”是“A與B互為對立事件”的充分不必要條件

  B．設具有線性相關關系的兩個變量x,y的相關系數為r,則|r|越接近于0，x,y之間線性相關程度越強

  C．已知隨機變量X的方差為D（X），則D（2X-3）=2D（X）-3

  D．若X～N（1，σ2），P（X＞2）=0.2，則P（0＜X＜1）=0.3
  組卷：40引用：1難度：0.5

  解析

• 5．已知

  a

  ，

  b

  是單位向量，且

  a

  +

  b

  =

  （

  1

  ，-

  1

  ）

  ，若向量

  c

  =

  a

  -

  b

  ，則

  a

  與

  c

  的夾角為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  組卷：455引用：4難度：0.8

  解析

• 6．設x∈（0，

  π

  2

  ），則事件“2sinx＞tanx”發生的概率為（　　）

  A． 1 3

  B． 1 2

  C． 2 3

  D． 2 3 π
  組卷：89引用：5難度：0.8

  解析

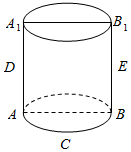• 7．如圖，圓柱OO₁的軸截面ABB₁A₁是正方形，D，E分別是AA₁和BB₁的中點，C是弧

  ?

  AB

  的中點，則經過C、D、E的平面與圓柱OO₁側面相交所得到的曲線的離心率是（　　）

  A．1

  B． 2 2

  C． 2

  D． 6 2
  組卷：81引用：3難度：0.7

  解析

[選修4-4：坐標系與參數方程]

• 22．在平面直角坐標系中，直線l的參數方程為

  x = tcosα

  y = tsinα

  （t為參數，0≤α＜π）．以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C的極坐標方程為ρ²-4=4ρcosθ-2ρsinθ．
  （Ⅰ）寫出曲線C的直角坐標方程；
  （Ⅱ）若直線l與曲線C交于A，B兩點，且AB的長度為2

  5

  ，求直線l的普通方程．
  組卷：266引用：11難度：0.8

  解析

[選修4-5：不等式選講]

• 23．已知關于x的不等式|x-2|-|x-3|≤m對x∈R恒成立．
  （1）求實數m的最小值；
  （2）若a,b,c為正實數，k為實數m的最小值，且

  1

  a

  +

  1

  2

  b

  +

  1

  3

  c

  =k,求證：a+2b+3c≥9．
  組卷：43引用：4難度：0.3

  解析