當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年黑龍江省齊齊哈爾市恒昌中學(xué)高三（上）期中數(shù)學(xué)試卷

發(fā)布：2024/10/5 7:0:1

一、單選題（本大題共8個(gè)小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.）

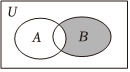1．已知全集U=R，集合A={x|x≥2或x≤-3}，B={x|0≤x≤4}，則Venn圖中陰影部分表示的集合為（　　）
A．[0，2） B．[0，3） C．（2，4] D．（3，4]
組卷：236引用：6難度：0.7
解析
2．存在量詞命題“?x∈R，x²≤|x|”的否定是（　　）
A．?x∈R，x²≥|x| B．?x∈R，x²＞|x| C．?x∈R，x²＞|x| D．?x∈R，x²≥|x|
組卷：46引用：13難度：0.9
解析
3．已知向量
a
=
（
2
，
0
）
，
b
=
（
1
2
，
3
2
）
，則
b
?
（
a
-
b
）
=（　　）
A．3 B．
1
+
3
C．1 D．0
組卷：419引用：4難度：0.8
解析
4．已知
a
=
（
-
2
，-
1
）
，
b
=
（
1
，
2
）
，若向量
a
在向量
b
上的投影向量為
c
，則
c
=（　　）
A．
（
-
4
5
5
，-
8
5
5
）
B．
（
4
5
5
，-
8
5
5
）
C．
（
-
4
5
，-
8
5
）
D．
（
-
8
5
，-
4
5
）
組卷：163引用：7難度：0.8
解析
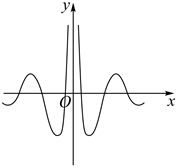5．著名數(shù)學(xué)家華羅庚先生曾說(shuō)過(guò)：“數(shù)缺形時(shí)少直觀，形缺數(shù)時(shí)難入微，數(shù)形結(jié)合百般好，隔裂分家萬(wàn)事休．”在數(shù)學(xué)的學(xué)習(xí)和研究中，我們經(jīng)常用函數(shù)的圖象來(lái)研究函數(shù)的性質(zhì)，也經(jīng)常用函數(shù)的解析式來(lái)琢磨函數(shù)的圖象特征，如某體育品牌的LOGO為，可抽象為如圖所示的軸對(duì)稱的優(yōu)美曲線，下列函數(shù)中，其圖象大致可“完美”局部表達(dá)這條曲線的函數(shù)是（　　）
A．
f
（
x
）
=
sin
5
x
2
-
x
-
2
x
B．
f
（
x
）
=
cos
5
x
2
-
x
-
2
x
C．
f
（
x
）
=
cos
5
x
|
2
x
-
2
-
x
|
D．
f
（
x
）
=
sin
5
x
|
2
x
-
2
-
x
|
組卷：37引用：3難度：0.7
解析
6．如圖，從氣球A上測(cè)得正前方的河流的兩岸B，C的俯角分別為75°，30°，若河流的寬度BC是60，則此時(shí)氣球的高度等于（　　）
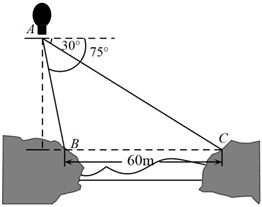
A．
15
（
3
-
1
）
B．
15
（
3
+
1
）
C．
30
（
3
-
1
）
D．
30
（
3
+
1
）
組卷：165引用：3難度：0.5
解析
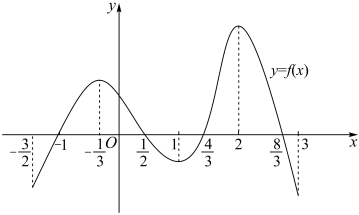7．已知函數(shù)f（x）在定義域
（
-
3
2
，
3
）
內(nèi)可導(dǎo)，其圖象如圖所示．記y=f（x）的導(dǎo)函數(shù)為y=f'（x），則不等式xf'（x）≤0的解集為（　　）
A．
（
-
3
2
，-
1
3
]
∪
[
0
，
1
]
∪
[
2
，
3
）
B．
[
-
1
3
，
0
]
∪
[
1
，
2
]
∪
[
8
3
，
3
）
C．
[
-
1
3
，
1
]
∪
[
2
，
3
）
D．
（
-
3
2
，-
1
3
）
∪
[
1
2
，
4
3
]
∪
[
8
3
，
3
）
組卷：285引用：4難度：0.7
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

四、解答題（本大題共6個(gè)小題，共70分，解答時(shí)應(yīng)寫(xiě)出必要的文字說(shuō)明、證明過(guò)程或演算步驟）

21．已知向量
m
=（2cosωx,
3
），
n
=（sinωx,2cos²ωx-1）（ω＞0），f（x）=
m
?
n
，
（1）若函數(shù)y=f（x）的最小正周期為π，求函數(shù)y=f（x）的單調(diào)減區(qū)間．
（2）若函數(shù)y=f（x）在
（
0
，
π
2
）
上有且只有一個(gè)極值點(diǎn)，求ω的取值范圍．
組卷：39引用：2難度：0.6
解析
22．已知函數(shù)f（x）=e^2x+（a+2）e^x+ax.
（Ⅰ）討論f（x）的單調(diào)性；
（Ⅱ）當(dāng)a＞0時(shí)，設(shè)x₀為f（x）的零點(diǎn)，證明：
ln
2
a
4
a
+
5
＜
x
0
＜
-
1
e
．
組卷：98引用：2難度：0.3
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測(cè)評(píng) 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A．（ - 4 5 5 ，- 8 5 5 ）	B．（ 4 5 5 ，- 8 5 5 ）
C．（ - 4 5 ，- 8 5 ）	D．（ - 8 5 ，- 4 5 ）

A． f （ x ） = sin 5 x 2 - x - 2 x	B． f （ x ） = cos 5 x 2 - x - 2 x
C． f （ x ） = cos 5 x \| 2 x - 2 - x \|	D． f （ x ） = sin 5 x \| 2 x - 2 - x \|

2023-2024學(xué)年黑龍江省齊齊哈爾市恒昌中學(xué)高三（上）期中數(shù)學(xué)試卷

一、單選題（本大題共8個(gè)小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.）

1．已知全集U=R，集合A={x|x≥2或x≤-3}，B={x|0≤x≤4}，則Venn圖中陰影部分表示的集合為（ ）

2．存在量詞命題“?x∈R，x2≤|x|”的否定是（ ）

3．已知向量a=（2，0），b=（12，32），則b?（a-b）=（ ）

4．已知a=（-2，-1），b=（1，2），若向量a在向量b上的投影向量為c，則c=（ ）

6．如圖，從氣球A上測(cè)得正前方的河流的兩岸B，C的俯角分別為75°，30°，若河流的寬度BC是60，則此時(shí)氣球的高度等于（ ）

7．已知函數(shù)f（x）在定義域（-32，3）內(nèi)可導(dǎo)，其圖象如圖所示．記y=f（x）的導(dǎo)函數(shù)為y=f'（x），則不等式xf'（x）≤0的解集為（ ）

四、解答題（本大題共6個(gè)小題，共70分，解答時(shí)應(yīng)寫(xiě)出必要的文字說(shuō)明、證明過(guò)程或演算步驟）

22．已知函數(shù)f（x）=e2x+（a+2）ex+ax.（Ⅰ）討論f（x）的單調(diào)性；（Ⅱ）當(dāng)a＞0時(shí)，設(shè)x0為f（x）的零點(diǎn)，證明：ln2a4a+5＜x0＜-1e．

1．已知全集U=R，集合A={x|x≥2或x≤-3}，B={x|0≤x≤4}，則Venn圖中陰影部分表示的集合為（　　）

2．存在量詞命題“?x∈R，x²≤|x|”的否定是（　　）

3．已知向量
a
=
（
2
，
0
）
，
b
=
（
1
2
，
3
2
）
，則
b
?
（
a
-
b
）
=（　　）

4．已知
a
=
（
-
2
，-
1
）
，
b
=
（
1
，
2
）
，若向量
a
在向量
b
上的投影向量為
c
，則
c
=（　　）

6．如圖，從氣球A上測(cè)得正前方的河流的兩岸B，C的俯角分別為75°，30°，若河流的寬度BC是60，則此時(shí)氣球的高度等于（　　）

7．已知函數(shù)f（x）在定義域
（
-
3
2
，
3
）
內(nèi)可導(dǎo)，其圖象如圖所示．記y=f（x）的導(dǎo)函數(shù)為y=f'（x），則不等式xf'（x）≤0的解集為（　　）

22．已知函數(shù)f（x）=e^2x+（a+2）e^x+ax.
（Ⅰ）討論f（x）的單調(diào)性；
（Ⅱ）當(dāng)a＞0時(shí)，設(shè)x₀為f（x）的零點(diǎn)，證明：
ln
2
a
4
a
+
5
＜
x
0
＜
-
1
e
．