2021-2022學年北京市101中學九年級(上)開學數學試卷
發布:2024/4/20 14:35:0
一、選擇題.本大題共16分,每題2分.
-
1.備受關注的北京環球度假區宣布將于2021年9月1日正式開啟試運行.根據規劃,北京環球影城建成后一期預計年接待游客超過1000萬人次,將1000萬用科學記數法表示為( )
A.0.1×104 B.1.0×103 C.1.0×106 D.1.0×107 組卷:472引用:2難度:0.7 -
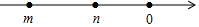 2.實數m,n在數軸上的對應點如圖所示,則下列各式子正確的是( )
2.實數m,n在數軸上的對應點如圖所示,則下列各式子正確的是( )A.m>n B.-n>|m| C.-m>|n| D.|m|<|n| 組卷:5373引用:35難度:0.7 -
3.已知正多邊形的一個外角為36°,則該正多邊形的邊數為( )
A.12 B.10 C.8 D.6 組卷:2195引用:33難度:0.8 -
4.函數y=
,自變量x的取值范圍是( )x-2A.x>2 B.x<2 C.x≥2 D.x≤2 組卷:4181引用:94難度:0.9 -
 5.如圖,將一塊含有30°角的直角三角板的兩個頂點分別放在直尺的兩條平行對邊上,若∠α=135°,則∠β等于( )
5.如圖,將一塊含有30°角的直角三角板的兩個頂點分別放在直尺的兩條平行對邊上,若∠α=135°,則∠β等于( )A.45° B.60° C.75° D.85° 組卷:1630引用:19難度:0.8 -
 6.已知銳角∠AOB,如圖,
6.已知銳角∠AOB,如圖,
(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作,交射線OB于點D,連接CD;?MN
(2)分別以點C,D為圓心,CD長為半徑作弧,兩弧交于點P,連接CP,DP;
(3)作射線OP交CD于點Q.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )A.CP∥OB B.CP=2QC C.∠AOP=∠BOP D.CD⊥OP 組卷:454引用:12難度:0.5 -
7.勾股定理是人類最偉大的科學發現之一,在我國古算書《周髀算經》中早有記載.如圖1,以直角三角形的各邊為邊分別向外作正方形,再把較小的兩張正方形紙片按圖2的方式放置在最大正方形內.若知道圖中陰影部分的面積,則一定能求出( )
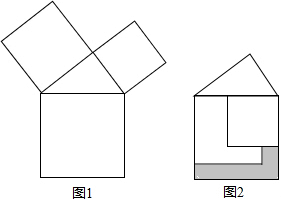
A.直角三角形的面積 B.最大正方形的面積 C.較小兩個正方形重疊部分的面積 D.最大正方形與直角三角形的面積和 組卷:7094引用:39難度:0.6 -
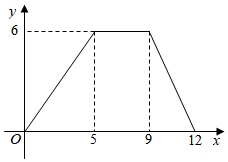 8.如圖,是一對變量滿足的函數關系的圖象,有下列3個不同的問題情境:
8.如圖,是一對變量滿足的函數關系的圖象,有下列3個不同的問題情境:
①小明騎車以400m/min的速度勻速騎了5min,在原地休息了4min,然后以500m/min的速度勻速騎回出發地,設時間為x min,離出發地的距離為y km;
②有一個容積為6L的開口空桶,小亮以1.2L/min的速度勻速向這個空桶注水,注5min后停止,等4min后,再以2L/min的速度勻速倒空桶中的水,設時間為x min,桶內的水量為y L;
③矩形ABCD中,AB=4,BC=3,動點P從點A出發,依次沿對角線AC,邊CD,邊DA運動至點A停止,設點P的運動路程為x,當點P與點A不重合時,y=S△ABP;當點P與點A重合時,y=0.
其中,符合圖中所示函數關系的問題情境為( )A.② B.②③ C.①③ D.①② 組卷:379引用:1難度:0.5
二、填空題:本大題共16分,每題2分.
-
9.已知x=2y+3,則代數式4x-8y+9的值是.
組卷:3150引用:45難度:0.8
三、解答題:本題共68分,第17-21題,每小題5分,第22-24,每小題5分,25題5分,第26-27題,每小題5分,第28題6分
-
27.在△ABC中,∠A=90°,AB=AC.

(1)如圖1,△ABC的角平分線BD,CE交于點Q,請判斷“QB=QA”是否正確; (填“是”或“否”);2
(2)點P是△ABC所在平面內的一點,連接PA,PB,且PB=PA.2
①如圖2,點P在△ABC內,∠ABP=30°,求∠PAB的大小;
②如圖3,點P在△ABC外,連接PC,設∠APC=α,∠BPC=β,求α+β的值.組卷:124引用:1難度:0.2 -
28.【定義】
在平面直角坐標系xOy中,如果點A,C為某個菱形的一組對角的頂點,且點A,C在直線y=x上,那么稱該菱形為點A,C的“最佳菱形”.如圖是點A,C的“最佳菱形”的一個示意圖.
【運用】
已知點M的坐標為(1,1),點P的坐標為(3,3).
(1)點E(1,3),F(2,1),G(4,0)中,能夠成為點M,P的“最佳菱形”的頂點的是
(2)如果四邊形MNPQ是點M,P的“最佳菱形”.
①當點N的坐標為(3,1)時,求四邊形MNPQ的面積;
②當四邊形MNPQ的面積為8,且與直線y=x+b有公共點時,求b的取值范圍(直接寫出結果).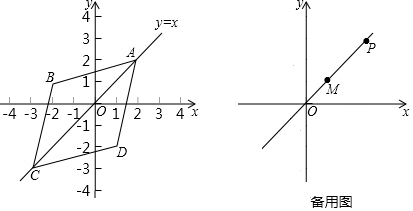 組卷:91引用:1難度:0.6
組卷:91引用:1難度:0.6


