2009-2010學年數學暑假作業16

一、填空題

• 1．橢圓

  x

  2

  log

  a

  8

  +

  y

  2

  9

  =

  1

  的離心率為

  1

  2

  ，則a=

  ．
  組卷：10引用：3難度：0.7

  解析

• 2．若

  x

  2

  |

  k

  |

  -

  2

  +

  y

  2

  1

  -

  k

  =

  -

  1

  表示焦點在y軸上的雙曲線，則它的半焦距c的取值范圍是

  ．
  組卷：29引用：5難度：0.7

  解析

• 3．以坐標軸為對稱軸、漸近線互相垂直、兩準線間距離為2的雙曲線方程是

  ．
  組卷：18引用：1難度：0.9

  解析

• 4．過雙曲線x²-y²=8的右焦點F₂有一條弦PQ，PQ=7，F₁是左焦點，那么△F₁PQ的周長為

  ．
  組卷：10引用：1難度：0.9

  解析

• 5．高5m和3m的旗桿在水平地面上，如果把兩旗桿底部的坐標分別定為A（-5，0），B（5，0），則地面上桿頂仰角相等的點的軌跡是

  ．
  組卷：3引用：1難度：0.7

  解析

• 6．直線l過點

  （

  2

  ，

  0

  ）

  且與雙曲線x²-y²=2僅有一個公共點，這樣的直線有

  條．
  組卷：54引用：4難度：0.7

  解析

二、解答題（共6小題，滿分0分）

• 19．設橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左焦點為F₁（-2，0），左準線l₁與x軸交于點N（-3，0），過點N且傾斜角為30°的直線l交橢圓于A、B兩點．
  （1）求直線l和橢圓的方程；
  （2）求證：點F₁（-2，0）在以線段AB為直徑的圓上；
  （3）在直線l上有兩個不重合的動點C、D，以CD為直徑且過點F₁的所有圓中，求面積最小的圓的半徑長．
  組卷：23引用：4難度：0.5

  解析

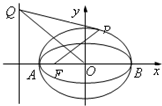• 20．已知圓O：x²+y²=2交x軸于A，B兩點，曲線C是以AB為長軸，離心率為

  2

  2

  的橢圓，其左焦點為F．若P是圓O上一點，連接PF，過原點O作直線PF的垂線交橢圓C的左準線于點Q．
  （1）求橢圓C的標準方程；
  （2）若點P的坐標為（1，1），求證：直線PQ與圓O相切；
  （3）試探究：當點P在圓O上運動時（不與A、B重合），直線PQ與圓O是否保持相切的位置關系？若是，請證明；若不是，請說明理由．
  組卷：97引用：19難度：0.5

  解析