當前位置：試卷中心 > 試卷詳情

2023年河南省TOP二十名校高考數(shù)學調研試卷（文科）（2月份）

發(fā)布：2024/4/20 14:35:0

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．設集合
A
=
{
x
|
1
＜
x
＜
2
}
，B={0，2，4，6}，則A∩B=（　　）
A．{0} B．{2} C．{2，4} D．{0，2，4}
組卷：27引用：3難度：0.7
解析
2．若z=1+i,則
|
z
z
-
1
|
=（　　）
A．
2
2
B．1 C．-
2
D．2
組卷：84引用：1難度：0.8
解析
3．已知向量
a
，
b
滿足
|
a
|
=
2
|
b
|
=
2
，
|
a
-
b
|
=
3
，則
?
a
，
b
?
=（　　）
A．30° B．45° C．60° D．90°
組卷：386引用：3難度：0.7
解析
4．已知等差數(shù)列{a_n}的前n項和為S_n，S₂=-4，a₂+a₃=-8，則{a_n}的公差為（　　）
A．-2 B．-1 C．1 D．2
組卷：204引用：1難度：0.8
解析
5．經(jīng)濟學專業(yè)的學生們?yōu)檠芯苛魍ㄙM率y和銷售額x（單位：千萬元）的關系，對同類型10家企業(yè)的相關數(shù)據(jù)（x_i，y_i）（i=1，2，?，10）進行整理，并得到如圖散點圖：

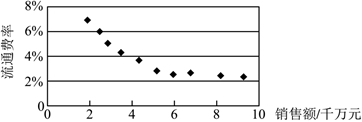
由此散點圖，在2千萬元至1億元之間，下面四個回歸方程類型中最適宜作為流通費率y和銷售額x的回歸方程類型的是（　　）
A．y=ax+b B．y=ax²+b C．y=ae^x+b D．y=alnx+b
組卷：142引用：3難度：0.7
解析
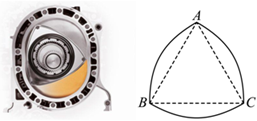6．轉子發(fā)動機采用三角轉子旋轉運動來控制壓縮和排放．如圖，三角轉子的外形是有三條側棱的曲面棱柱，且側棱垂直于底面，底面是以正三角形的三個頂點為圓心，正三角形的邊長為半徑畫圓構成的曲面三角形，正三角形的頂點稱為曲面三角形的頂點，側棱長為曲面棱柱的高，記該曲面棱柱的底面積為S，高為h,已知曲面棱柱的體積V=Sh,若
AB
=
6
，h=1，則曲面棱柱的體積為（　　）
A．
3
π
-
3
3
B．
2
π
-
2
2
C．
3
π
-
2
2
D．
2
π
-
3
3
組卷：215引用：5難度：0.7
解析
7．已知拋物線C：y²=2px（p＞0）焦點為F，準線為l,點A（3，
2
3
）在C上，直線AF與l交于點B，則
|
AF
|
|
BF
|
=（　　）
A．1 B．
2
C．
3
D．2
組卷：44引用：1難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

（二）選考題：共10分。請考生從22、23題中任選一題做答，如果多做，則按所做的第一題計分。[選修4-4：坐標系與參數(shù)方程]

22．在直角坐標系xOy中，曲線C₁，C₂的參數(shù)方程分別為
x
=
2
t
y
=
2
t
2
（t為參數(shù)），
x
=
2
cosθ
y
=
2
+
2
sinθ
（θ為參數(shù)）．
（1）將C₁，C₂的參數(shù)方程化為普通方程；
（2）以坐標原點為極點，x軸正半軸為極軸建立極坐標系，直線l的極坐標方程為
ρsin
（
α
-
θ
）
=
2
sin
（
α
-
π
4
）
（
0
≤
α
＜
π
）
，若直線l與C₁，C₂共有三個交點，求α．
組卷：73引用：2難度：0.6
解析