2021-2022學(xué)年四川省成都實(shí)驗(yàn)外國(guó)語(yǔ)學(xué)校高一（下）第一次段考數(shù)學(xué)試卷

一、選擇題：（本大題共12個(gè)小題，每小題5分，共60分，在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)是符合題目要求的選項(xiàng)）

• 1．設(shè)全集U={1，2，3，4，5，6}，A={1，2}，B={2，3，4}，則A∩（?_UB）=（　　）

  A．{1，2，5，6}

  B．{1，2，3，4}

  C．{2}

  D．{1}
  組卷：129引用：7難度：0.9

  解析

• 2．向量

  a

  =

  （

  -

  1

  ，

  1

  ）

  在向量

  b

  =

  （

  -

  3

  ，-

  4

  ）

  上的投影為（　　）

  A． 2 2

  B． - 2 2

  C． 1 5

  D． - 1 5
  組卷：5引用：1難度：0.7

  解析

• 3．設(shè)a=sin（-810°），b=tan（-

  33

  π

  8

  ），c=lg

  1

  5

  ，則（　　）

  A．a(chǎn)＜b＜c

  B．a(chǎn)＜c＜b

  C．b＜c＜a

  D．c＜a＜b
  組卷：224引用：3難度：0.7

  解析

• 4．已知

  α

  ∈

  （

  0

  ，

  π

  ）

  ，

  tanα

  =

  1

  2

  ，則sin2α=（　　）

  A． 1 5

  B． 2 5

  C． 4 5

  D． 12 25
  組卷：52引用：2難度：0.7

  解析

• 5．函數(shù)f（x）=log₂|x|+cosx的大致圖象是（　　）

  A．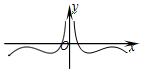

  B．

  C．

  D．
  組卷：110引用：4難度：0.8

  解析

• 6．如圖所示，在△ABC中，AD為BC邊上的中線，E為AD的中點(diǎn)，則

  EB

  =（　　）

  A． 3 4 AB - 1 4 AC

  B． 1 4 AB - 3 4 AC

  C． 3 4 AB + 1 4 AC

  D． 1 4 AB + 3 4 AC
  組卷：2048引用：9難度：0.8

  解析

• 7．為了得到函數(shù)y=2cos2x的圖象，只需把函數(shù)

  y

  =

  3

  sin

  2

  x

  +

  cos

  2

  x

  的圖象（　　）

  A．向左平移 π 3 個(gè)單位長(zhǎng)度	B．向右平移 π 3 個(gè)單位長(zhǎng)度
  C．向左平移 π 6 個(gè)單位長(zhǎng)度	D．向右平移 π 6 個(gè)單位長(zhǎng)度
  組卷：3引用：1難度：0.7

  解析

三、解答題：（本大題共6個(gè)小題，共70分．解答應(yīng)寫出文字說(shuō)明，證明過(guò)程或演算步驟）

• 21．已知

  a

  =

  （

  2

  cosx

  ,

  2

  sinx

  ）

  ，

  b

  =

  （

  sin

  （

  x

  -

  π

  6

  ）

  ，

  cos

  （

  x

  -

  π

  6

  ）

  ）

  ，

  a

  與

  b

  的夾角為θ，函數(shù)f（x）=cosθ．
  （1）求函數(shù)f（x）最小正周期和對(duì)稱中心；
  （2）若銳角△ABC中，角A，B，C的對(duì)邊分別為a,b,c,且f（A）=1，求

  b

  +

  c

  a

  的取值范圍．
  組卷：106引用：3難度：0.5

  解析

• 22．定義非零向量

  OM

  =

  （

  a

  ,

  b

  ）

  的“相伴函數(shù)”為f（x）=asinx+bcosx,（x∈R），向量

  OM

  =

  （

  a

  ,

  b

  ）

  稱為函數(shù)f（x）=asinx+bcosx（x∈R）的“相伴向量”（其中點(diǎn)O為坐標(biāo)原點(diǎn)）．
  （1）設(shè)函數(shù)

  h

  （

  x

  ）

  =

  2

  sin

  （

  π

  3

  -

  x

  ）

  -

  cos

  （

  π

  6

  +

  x

  ）

  ，求函數(shù)h（x）的“相伴向量”

  OM

  的坐標(biāo)；
  （2）記

  OM

  =

  （

  0

  ，

  2

  ）

  的“相伴函數(shù)”為f（x），設(shè)函數(shù)

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  +

  2

  3

  |

  sinx

  |

  -

  1

  ，x∈[0，2π]，若方程g（x）=k有四個(gè)不同實(shí)數(shù)根，求實(shí)數(shù)k的取值范圍；
  （3）已知點(diǎn)M（a,b），（b≠0）滿足條件：

  b

  a

  ∈

  （

  0

  ，

  3

  ]

  ，且向量

  OM

  的“相伴函數(shù)”f（x）在x=x₀時(shí)取得最大值，當(dāng)點(diǎn)M運(yùn)動(dòng)時(shí)，求tan2x₀的取值范圍．
  組卷：74引用：3難度：0.5

  解析