2020-2021學(xué)年福建省泉州五中高二（上）期中數(shù)學(xué)試卷

一、單項選擇題（本大題共8個小題，每小題5分，共40分.下列各題給出的四個選項中只有一個符合要求）

• 1．已知命題P：?x∈R，x＞sinx,則命題p的否定為（　　）

  A．￢p：?x0∈R，x0＜Sinx0	B．￢p：?x∈R，x＜sinx
  C．￢p：?x0∈R，x0≤sinx0	D．￢p：?x∈R，x≤sinx
  組卷：4引用：2難度：0.8

  解析

• 2．設(shè)

  u

  =（-2，2，t），

  v

  =（6，-4，4）分別是平面α，β的法向量．若α⊥β，則t等于（　　）

  A．6

  B．5

  C．4
  組卷：181引用：3難度：0.8

  解析

• 3．m=-2是直線（2-m）x+my+3=0與直線x-my-3=0垂直的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．非充分也非必要條件
  組卷：28引用：11難度：0.9

  解析

• 4．動點A在圓x²+y²=1上移動時，它與定點B（3，0）連線的中點的軌跡方程是（　　）

  A．（x+3）2+y2=4	B．（x-3）2+y2=1
  C．（x+ 3 2 ）2+y2=1	D．（2x-3）2+4y2=1
  組卷：109引用：6難度：0.8

  解析

• 5．過直線y=x+1上的點P作圓C：（x-1）²+（y-6）²=2的兩條切線l₁，l₂，當(dāng)直線l₁，l₂關(guān)于直線y=x+1對稱時，|PC|=（　　）

  A．3

  B．2 2

  C．1+ 2

  D．2
  組卷：412引用：9難度：0.7

  解析

• 6．若圓x²+y²=4上恰有2個點到直線y=x+b的距離等于1，則b的取值范圍是（　　）

  A． （ - 2 2 ，- 2 ） ∪ （ 2 ， 2 2 ）	B． （ - 3 2 ，- 2 ） ∪ （ 2 ， 3 2 ）
  C． （ - 2 ， 2 ）	D． （ - 3 2 ， 3 2 ）
  組卷：247引用：4難度：0.5

  解析

• 7．已知圓C₁：x²+y²-kx-y=0和圓C₂：x²+y²-2ky-1=0的公共弦所在的直線恒過定點M，且點M在直線mx+ny=2上，則

  m

  2

  +

  n

  2

  的最小值為（　　）

  A． 1 5

  B． 5 5

  C． 2 5 5

  D． 4 5
  組卷：635引用：6難度：0.5

  解析

四、解答題（每題13分，共5題，共65分）

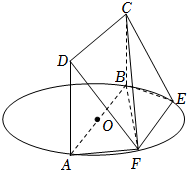• 21．如圖，AB為圓O的直徑，點E、F在圓O上，AB∥EF，矩形ABCD和圓O所在的平面互相垂直．已知AB=2，EF=1．
  （1）求證：直線BF⊥平面DAF；
  （2）當(dāng)AD的長為何值時，二面角C-EF-A的大小為30°？
  組卷：5引用：1難度：0.6

  解析

• 22．在平面直角坐標(biāo)系xOy中，已知直線l：y=kx+3+8

  2

  和圓C₁：x²+y²+8x+F=0．當(dāng)k=2

  2

  時，直線l被圓C₁截得的弦長為2

  3

  ．
  （1）求圓C₁的方程；
  （2）直線l與圓C₁交于A，B兩點，求△OAB面積的最大值，并求出此時k的值；
  （3）設(shè)圓C₁和x軸相交于W，T兩點，點P為圓C₁上不同于W，T的任意一點，直線PW，PT交y軸于M，N兩點．當(dāng)點P變化時，以MN為直徑的圓C₂是否經(jīng)過圓C₁內(nèi)一定點？請證明你的結(jié)論．
  組卷：12引用：1難度：0.5

  解析