2023-2024學年湖北省武漢四十九中高三（上）月考數學試卷（9月份）（二）

一、選擇題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．已知集合A={x|x²-2x-3＜0}，B={y|y=e^x}，則A∩B=（　　）

  A．?

  B．（-1，+∞）

  C．（0，3）

  D．（1，3）
  組卷：57引用：7難度：0.7

  解析

• 2．已知復數z=

  2

  i

  1

  -

  i

  ，則下列結論正確的是（　　）

  A．z在復平面對應的點位于第三象限

  B．z的虛部是i

  C．|z|= 2

  D． z =1+i
  組卷：186引用：7難度：0.7

  解析

• 3．已知△ABC的外接圓圓心為O，且

  AO

  =

  AB

  +

  AC

  ，則

  BA

  在

  BC

  上的投影向量為（　　）

  A． 1 2 BC

  B． - 1 2 BC

  C． 1 4 BC

  D． - 1 4 BC
  組卷：33引用：3難度：0.8

  解析

• 4．已知函數

  f

  （

  x

  ）

  =

  x 2 + ax + 1 ， x ≥ 1

  a x 2 + x + 1 ， x ＜ 1

  則“-2≤a≤0”是“f（x）在R上單調遞增”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：130引用：7難度：0.7

  解析

• 5．若直線l：kx-y-2=0與曲線

  C

  ：

  1

  -

  （

  y

  -

  1

  ）

  2

  =

  x

  -

  1

  有兩個交點，則實數k的取值范圍是（　　）

  A． （ 4 3 ， 2 ]	B． （ 4 3 ， 4 ）
  C． [ - 2 ， 4 3 ） ∪ （ 4 3 ， 2 ]	D． （ 4 3 ， + ∞ ）
  組卷：486引用：36難度：0.6

  解析

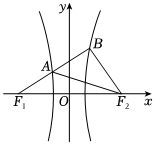• 6．如圖所示，點F₁，F₂是雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點，雙曲線C的右支上存在一點B滿足BF₁⊥BF₂，BF₁與雙曲線C的左支的交點A平分線段BF₁，則雙曲線C的漸近線斜率為（　　）

  A．±3

  B． ± 2 3

  C． ± 13

  D． ± 15
  組卷：279引用：5難度：0.6

  解析

• 7．已知S_n是等比數列{a_n}的前n項和，且

  S

  n

  =

  2

  n

  +

  1

  +

  a

  ，則a₁a₂+a₂a₃+?+a₁₀a₁₁=（　　）

  A． 2 23 - 8 3

  B． 2 13 - 8 3

  C． 2 20 - 1 3

  D． 2 25 - 8 3
  組卷：385引用：6難度：0.6

  解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明，證明過程或演算步驟.

• 21．甲、乙兩人進行象棋比賽，賽前每人發3枚籌碼．一局后負的一方，需將自己的一枚籌碼給對方；若平局，雙方的籌碼不動，當一方無籌碼時，比賽結束，另一方最終獲勝．由以往兩人的比賽結果可知，在一局中甲勝的概率為0.3、乙勝的概率為0.2．
  （1）第一局比賽后，甲的籌碼個數記為X，求X的分布列和期望；
  （2）求四局比賽后，比賽結束的概率；
  （3）若P_i（i=0，1，?，6）表示“在甲所得籌碼為i枚時，最終甲獲勝的概率”，則P₀=0，P₆=1．證明：{P_i+1-P_i}（i=0，1，2，?，5）為等比數列．
  組卷：279引用：5難度：0.4

  解析

• 22．已知定點F（1，0），定直線l：x=-1，動圓M過點F，且與直線l相切．
  （1）求動圓的圓心M所在軌跡C的方程；
  （2）已知點P（t,-1）是軌跡C上一點，點A，B是軌跡C上不同的兩點（點A，B均不與點P重合），設直線AP，BP的斜率分別為k₁、k₂，且滿足

  k

  1

  +

  k

  2

  =

  -

  8

  5

  ，證明：直線AB過定點，并求出定點的坐標．
  組卷：84引用：6難度：0.5

  解析