2023-2024學年山東省部分學校（中）高三（上）月考數學試卷（10月份）

一、單項選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題要求的。

• 1．下列各式中，值為

  -

  3

  4

  的是（　　）

  A．2sin15°?cos15°	B．cos215°-sin215°
  C．2sin215°-1	D． 1 2 - co s 2 15 °
  組卷：33引用：4難度：0.9

  解析

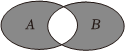• 2．如圖所示的韋恩圖中，A，B是非空集合，定義集合A#B為陰影部分表示的集合．若x,y∈R，A={x|y=

  2

  x

  -

  x

  2

  }，B={y|y=3^x，x＞0}，則A#B=（　　）

  A．{x|0＜x＜2}	B．{x|1＜x≤2}
  C．{x|0≤x≤1或x≥2}	D．{x|0≤x≤1或x＞2}
  組卷：130引用：19難度：0.9

  解析

• 3．將函數f（x）=2sin

  （

  ωx

  -

  π

  3

  ）

  （

  ω

  ＞

  0

  ）

  的圖象向左平移

  π

  3

  ω

  個單位，得到函數y=g（x）的圖象．若y=g（x）在[

  0

  ，

  π

  4

  ]上為增函數，則ω的最大值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：60引用：12難度：0.9

  解析

• 4．化簡（

  a

  2

  3

  b

  1

  2

  ）×（-

  3

  a

  1

  2

  b

  1

  3

  ）÷（

  1

  3

  a

  1

  6

  b

  5

  6

  ）的結果（　　）

  A．6a

  B．-a

  C．-9a

  D．9a2
  組卷：336引用：30難度：0.9

  解析

• 5．已知3^a=5^b=A，且

  1

  a

  +

  1

  b

  =2，則A的值是（　　）

  A．15

  B． 15

  C．± 15

  D．225
  組卷：434引用：24難度：0.9

  解析

• 6．給出下列命題①?x∈R，x²+1＞0；②?x∈N，x⁴≥1；③?x∈Z，x³＜1；④?x∈Q，x²≠2．其中真命題有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：7引用：3難度：0.8

  解析

• 7．若f（x）=-x²+ax+2+lg（2-|x|）（a∈R）是偶函數，且f（1-m）＜f（m），則實數m的取值范圍是（　　）

  A．（ 1 2 ，+∞）

  B．（-∞， 1 2 ）

  C．（ 1 2 ，2）

  D．（-1， 1 2 ）
  組卷：32引用：3難度：0.7

  解析

四、解答題：（本大題共6個小題，滿分70分，解答應寫出必要的文字說明、證明過程和演算步驟。）

• 21．已知函數f（x）=alnx-2ax+3（a≠0）．
  （1）求函數f（x）的極值；
  （2）若函數y=f（x）的圖象在x=2處的切線的斜率為

  3

  2

  ，

  g

  （

  x

  ）

  =

  1

  3

  x

  3

  +

  x

  2

  [

  f

  ′

  （

  x

  ）

  +

  m

  ]

  在區間（1，3）上不是單調函數，且當x∈（0，1]時f（x）不小于

  2

  3

  x

  3

  -

  2

  m

  ，求實數m的取值范圍．
  組卷：17引用：2難度：0.6

  解析

• 22．已知函數f（x）=lnx,g（x）=e^x（e^x=2.718…，e為自然對數的底數）
  （1）求函數F（x）=f（x）-g（x-1）的單調區間；
  （2）若不等式xf（x）-k（x+1）f[g（x-1）]≤0在區間[1，+∞）上恒成立，求實數k的取值范圍．
  組卷：18引用：6難度：0.5

  解析