2023年安徽省滁州市定遠中學高考數學預測試卷（6月份）

一、單選題（本大題共8小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．設集合A={x|4x²-13x＜0}，

  B

  =

  {

  y

  |

  y

  =

  x

  -

  2

  +

  3

  }

  ，則A∩B=（　　）

  A．（0，2]

  B．（0，3]

  C． [ 2 ， 13 4 ）

  D． [ 3 ， 13 4 ）
  組卷：87引用：2難度：0.7

  解析

• 2．若復數z滿足（1-i）z=|1+i|，則z的虛部是（　　）

  A．i

  B．1

  C． 2 2 i

  D． 2 2
  組卷：248引用：7難度：0.9

  解析

• 3．已知函數

  y

  =

  a

  x

  -

  3

  -

  2

  3

  （a＞0，且a≠1）的圖象恒過定點P．若點P在冪函數f（x）的圖象上，則冪函數f（x）的圖象大致是（　　）

  A．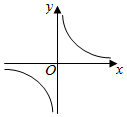

  B．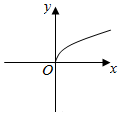

  C．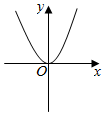

  D．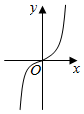
  組卷：181引用：6難度：0.6

  解析

• 4．已知數列{a_n}中，a₁=2，a_n+a_n+1=5，則數列{a_n}前11項的和S₁₁=（　　）

  A．22

  B．27

  C．28

  D．55
  組卷：77引用：1難度：0.7

  解析

• 5．已知函數

  f

  （

  x

  ）

  =

  1

  2

  x

  +

  2

  +

  2

  4

  x

  -

  4

  +

  1

  +

  1

  x

  -

  1

  ，則不等式f（2x+3）＞f（x²）的解集為（　　）

  A．（-2，1）∪（1，+∞）	B．（-1，1）∪（3，+∞）
  C． （ - 1 2 ， 1 ） ∪ （ 3 ， + ∞ ）	D．（-3，1）∪（3，+∞）
  組卷：115引用：3難度：0.6

  解析

• 6．已知橢圓

  x

  2

  a

  2

  1

  +

  y

  2

  b

  2

  1

  =1（a₁＞b₁＞0）的離心率為

  2

  2

  ，雙曲線

  x

  2

  a

  2

  2

  -

  y

  2

  b

  2

  2

  =1（a₂＞0，b₂＞0）與橢圓有相同的焦點F₁，F₂，M是兩曲線的一個公共點，若∠F₁MF₂=60°，則雙曲線的漸近線方程為（　　）

  A．y=± 2 2 x

  B．y=±x

  C．y=± 2 x

  D．y=± 3 x
  組卷：180引用：6難度：0.7

  解析

• 7．小林同學喜歡吃4種堅果：核桃、腰果、杏仁、榛子，他有5種顏色的“每日堅果”袋．每個袋子中至少裝1種堅果，至多裝4種堅果．小林同學希望五個袋子中所裝堅果種類各不相同，且每一種堅果在袋子中出現的總次數均為偶數，那么不同的方案數為（　　）

  A．20160

  B．20220

  C．20280

  D．20340
  組卷：1145引用：2難度：0.3

  解析

四、解答題（本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟）

• 21．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的實軸長為

  2

  2

  ，C的一條漸近線斜率為

  -

  2

  2

  ，直線l交C于P，Q兩點，點

  M

  （

  2

  a

  ,

  b

  ）

  在雙曲線C上．
  （1）若直線l過C的右焦點，且斜率為-1，求△PMQ的面積；
  （2）設P，Q為雙曲線C上異于點

  M

  （

  2

  a

  ,

  b

  ）

  的兩動點，記直線MP，MQ的斜率分別為k₁，k₂，若k₁+k₂=2k₁k₂，求證：直線PQ過定點．
  組卷：91引用：3難度：0.3

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  a

  2

  x

  2

  -

  x

  （

  lnx

  -

  b

  -

  1

  ）

  ，a,b∈R．
  （1）當b=-1時，討論函數f（x）的零點個數；
  （2）若f（x）在（0，+∞）上單調遞增，且c≤e^2a+b，求c的最大值．
  組卷：267引用：6難度：0.2

  解析