當前位置：試卷中心 > 試卷詳情

2022-2023學年湖北省問津聯合體高二（上）期中數學試卷

發布：2024/8/22 1:0:1

一、選擇題（共8小題，每小題5分，滿分40分）

1．直線x+
3
y-1=0的傾斜角為（　　）
A．30° B．60° C．120° D．150°
組卷：480引用：25難度：0.9
解析
2．已知橢圓
x
2
4
+y²=1，則該橢圓的焦距為（　　）
A．
3
B．2
3
C．
5
D．2
5
組卷：236引用：2難度：0.8
解析
3．已知直線l₁：（k-3）x+（4-k）y+1=0與l₂：2（k-3）x-2y+3=0平行，則k的值是（　　）
A．1或3 B．5 C．3或5 D．2
組卷：124引用：4難度：0.9
解析
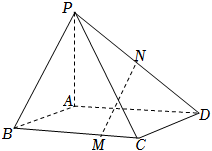4．已知四棱錐P-ABCD，底面ABCD為平行四邊形，M，N分別為棱BC，PD上的點，
CM
CB
=
1
3
，PN=ND，設
AB
=
a
，
AD
=
b
，
AP
=
c
，則向量
MN
用
{
a
，
b
，
c
}
為基底表示為（　　）
A．
a
+
1
3
b
+
1
2
c
B．
-
a
+
1
6
b
+
1
2
c
C．
a
-
1
3
b
+
1
2
c
D．
-
a
-
1
6
b
+
1
2
c
組卷：828引用：20難度：0.7
解析
5．如圖，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，∠ACB=90°，
BC
=
A
A
1
=
3
，AC=1，則異面直線AC₁與CB₁所成角的余弦值為（　　）
A．
2
3
B．
6
4
C．
3
2
D．
2
5
5
組卷：71引用：5難度：0.6
解析
6．若直線y=k（x-4）+2與曲線
x
=
4
-
y
2
恰有兩個交點，則實數k的取值范圍是（　　）
A．
[
1
，
4
3
）
B．
（
0
，
4
3
）
C．
[
1
，
5
3
）
D．
（
0
，
5
3
）
組卷：250引用：8難度：0.6
解析
7．已知點F₁（-2，0），圓F₂：（x-2）²+y²=36，點M是圓上一動點，線段MF₁的垂直平分線與MF₂交于點N．則點N的軌跡方程為（　　）
A．
x
2
9
-
y
2
2
=1 B．x-3y-2=0 C．x²+y²=36 D．
x
2
9
+
y
2
5
=1
組卷：19引用：1難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共6小題，滿分70分）

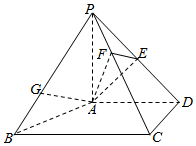21．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E為PD的中點，點F在PC上，且
PF
PC
=
1
3
．
（Ⅰ）求證：CD⊥平面PAD；
（Ⅱ）求二面角F-AE-P的余弦值；
（Ⅲ）設點G在PB上，且
PG
PB
=
2
3
．判斷直線AG是否在平面AEF內，說明理由．
組卷：5569引用：21難度：0.8
解析
22．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的長軸長是短軸長的
2
倍，且經過點（
2
，
1
）．
（1）求C的標準方程；
（2）已知C的右頂點為A，過C右焦點的直線l與C交于不同的兩點M，N，求△AMN面積的最大值．
組卷：43引用：6難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2022-2023學年湖北省問津聯合體高二（上）期中數學試卷

一、選擇題（共8小題，每小題5分，滿分40分）

1．直線x+3y-1=0的傾斜角為（ ）

2．已知橢圓x24+y2=1，則該橢圓的焦距為（ ）

3．已知直線l1：（k-3）x+（4-k）y+1=0與l2：2（k-3）x-2y+3=0平行，則k的值是（ ）

4．已知四棱錐P-ABCD，底面ABCD為平行四邊形，M，N分別為棱BC，PD上的點，CMCB=13，PN=ND，設AB=a，AD=b，AP=c，則向量MN用{a，b，c}為基底表示為（ ）

5．如圖，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，BC=AA1=3，AC=1，則異面直線AC1與CB1所成角的余弦值為（ ）

6．若直線y=k（x-4）+2與曲線x=4-y2恰有兩個交點，則實數k的取值范圍是（ ）

7．已知點F1（-2，0），圓F2：（x-2）2+y2=36，點M是圓上一動點，線段MF1的垂直平分線與MF2交于點N．則點N的軌跡方程為（ ）

四、解答題（共6小題，滿分70分）

22．已知橢圓C：x2a2+y2b2=1（a＞b＞0）的長軸長是短軸長的2倍，且經過點（2，1）．（1）求C的標準方程；（2）已知C的右頂點為A，過C右焦點的直線l與C交于不同的兩點M，N，求△AMN面積的最大值．

1．直線x+
3
y-1=0的傾斜角為（　　）

2．已知橢圓
x
2
4
+y²=1，則該橢圓的焦距為（　　）

3．已知直線l₁：（k-3）x+（4-k）y+1=0與l₂：2（k-3）x-2y+3=0平行，則k的值是（　　）

4．已知四棱錐P-ABCD，底面ABCD為平行四邊形，M，N分別為棱BC，PD上的點，
CM
CB
=
1
3
，PN=ND，設
AB
=
a
，
AD
=
b
，
AP
=
c
，則向量
MN
用
{
a
，
b
，
c
}
為基底表示為（　　）

5．如圖，在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，∠ACB=90°，
BC
=
A
A
1
=
3
，AC=1，則異面直線AC₁與CB₁所成角的余弦值為（　　）

6．若直線y=k（x-4）+2與曲線
x
=
4
-
y
2
恰有兩個交點，則實數k的取值范圍是（　　）

7．已知點F₁（-2，0），圓F₂：（x-2）²+y²=36，點M是圓上一動點，線段MF₁的垂直平分線與MF₂交于點N．則點N的軌跡方程為（　　）

22．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的長軸長是短軸長的
2
倍，且經過點（
2
，
1
）．
（1）求C的標準方程；
（2）已知C的右頂點為A，過C右焦點的直線l與C交于不同的兩點M，N，求△AMN面積的最大值．