當前位置：試卷中心 > 試卷詳情

2023年江蘇省淮安市淮安區中考數學一模試卷

發布：2024/4/20 14:35:0

一、選擇題（本大題共8小題，每小題3分，共24分．在每小題給出的四個選項中，恰有一項是符合題目要求的，請將正確選項前的字母代號填涂在答題卡相應位置上）

1．
-
1
2023
的倒數是（　　）
A．-2023 B．2023 C．
1
2023
D．
-
1
2023
組卷：1380引用：50難度：0.9
解析
2．下列式子中，計算正確的是（　　）
A．a³+a³=a⁶ B．（-a²）³=-a⁶
C．a²?a³=a⁶ D．（a+b）²=a²+b²
組卷：276引用：10難度：0.7
解析
3．下面的幾何體中，主視圖為三角形的是（　　）
A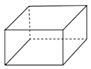． B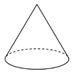． C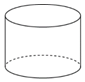． D．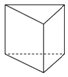
組卷：191引用：8難度：0.8
解析
4．在平面直角坐標系中，點P（1，-3）關于原點對稱的點的坐標是（　　）
A．（-1，3） B．（-3，1） C．（1，3） D．（3，-1）
組卷：316引用：12難度：0.9
解析
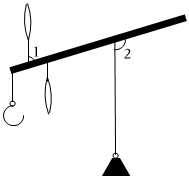5．一桿古秤在稱物時的狀態如圖所示，已知∠1=80°，則∠2=（　　）
A．20° B．80° C．100° D．120°
組卷：829引用：17難度：0.7
解析
6．如圖，在⊙O中，∠BOC=130°，點A在
?
BAC
上，則∠BAC的度數為（　　）
A．55° B．65° C．75° D．130°
組卷：1367引用：24難度：0.8
解析
7．下列命題是真命題的是（　　）
A．對頂角相等
B．平行四邊形的對角線互相垂直
C．三角形的內心是它的三條邊的垂直平分線的交點
D．三角分別相等的兩個三角形是全等三角形
組卷：333引用：3難度：0.7
解析
8．關于x的一元二次方程3x²-2x+m=0有兩根，其中一根為x=1，則這兩根之積為（　　）
A．
1
3
B．
2
3
C．1 D．-
1
3
組卷：1030引用：8難度：0.6
解析

二、填空題（本大題共8小題，每小題3分，共24分．不需要寫出解答過程，請把正確答案直接寫在答題卡相應位置上）

9．太陽光的速度是300 000 000米/秒，用科學記數法表示為
米/秒．
組卷：58引用：17難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共11小題，共102分．請在答題卡指定區域內作答，解答時應寫出必要的文字說明、證明過程或演算步驟）

26．綜合與實踐
“善思”小組開展“探究四點共圓的條件”活動，得出結論：對角互補的四邊形四個頂點共圓．該小組繼續利用上述結論進行探究．
提出問題：
如圖1，在線段AC同側有兩點B，D，連接AD，AB，BC，CD，如果∠B=∠D，那么A，B，C，D四點在同一個圓上．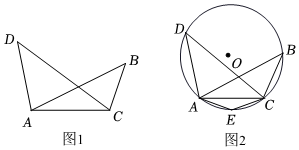

探究展示：
如圖2，作經過點A，C，D的⊙O，在劣弧AC上取一點E（不與A，C重合），連接AE，CE，則∠AEC+∠D=180°（依據1）
∵∠B=∠D
∴∠AEC+∠B=180°
∴點A，B，C，E四點在同一個圓上（對角互補的四邊形四個頂點共圓）
∴點B，D在點A，C，E所確定的⊙O上（依據2）
∴點A，B，C，D四點在同一個圓上
反思歸納：
（1）上述探究過程中的“依據1”、“依據2”分別是指什么？
依據1：
；依據2：
．
（2）如圖3，在四邊形ABCD中，∠1=∠2，∠3=45°，則∠4的度數為
．
拓展探究：
（3）如圖4，已知△ABC是等腰三角形，AB=AC，點D在BC上（不與BC的中點重合），連接AD．作點C關于AD的對稱點E，連接EB并延長交AD的延長線于F，連接AE，DE．
①求證：A，D，B，E四點共圓；
②若AB=2
2
，AD?AF的值是否會發生變化，若不變化，求出其值；若變化，請說明理由．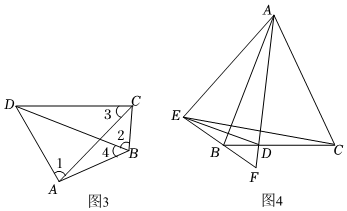
組卷：2385引用：5難度：0.3
解析
27．在平面直角坐標系xOy中，已知拋物線y=ax²+bx經過A（4，0），B（1，4）兩點．P是拋物線上一點，且在直線AB的上方．
（1）求拋物線的解析式；
（2）若△OAB面積是△PAB面積的2倍，求點P的坐標；
（3）如圖，OP交AB于點C，PD∥BO交AB于點D．記△CDP，△CPB，△CBO的面積分別為S₁，S₂，S₃．判斷
S
1
S
2
+
S
2
S
3
是否存在最大值．若存在，求出最大值；若不存在，請說明理由．
組卷：7151引用：15難度：0.2
解析