2012年第12屆“子陵杯”八年級數學競賽試卷（二試）
發布：2024/4/20 14:35:0
一．選擇題（本題有10個小題，每小題3分，共30分．）
-
1．下列運算正確的是（ ）
組卷：695引用：23難度：0.9 -
2．下列方程是一元二次方程的是（ ）
組卷：50引用：3難度：0.9 -
3．在下列命題中，是真命題的是（ ）
組卷：3471引用：68難度：0.9 -
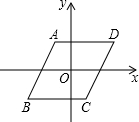4．如圖，以?ABCD對角線的交點為坐標原點，以平行于AD邊的直線為x軸，建立平面直角坐標系．若點D的坐標為（3，2），則點B的坐標為（ ）組卷：123引用：12難度：0.9 -
5．余姚某校為了了解學生在校午餐所需的時間，抽量了20名學生在校午餐所需時間，獲得如下的數據（單位：分）：10、12、15、8、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、16．若將這些數據以4分為組距進行分組，則組數是（ ）
組卷：147引用：1難度：0.9 -
6．順次連接等腰梯形各邊中點所圍成的四邊形是（ ）
組卷：542引用：53難度：0.9 -
7．有一天，某市一家珠寶店發生了一起盜竊案，盜走了價值10萬元珠寶，經過公安干警兩個多月的偵查，鎖定犯罪嫌疑人必是A、B、C、D四人中的一人，經審訊，四人提供了下面的口供．A說：“珠寶被盜那天，我在別的城市，所以我不可能作案”；B說：“D是偷盜珠寶的人”；C說：“B是偷盜犯，三天前我看見他在黑市上賣珠寶”；D說：“B同我有仇，有意誣陷我，我不是罪犯”．經過進一步調查取證，這四人只有一個人說的是真話．你知道犯罪嫌疑人是誰嗎？這四個人中誰說的是真話？（ ）
組卷：93引用：1難度：0.9 -
8．如圖，邊長為1的正方形ABCD繞點A逆時針旋轉30°到正方形AB′C′D′，圖中陰影部分的面積為（ ）組卷：3772引用：108難度：0.5 -
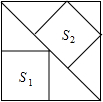9．如圖，大正方形中有2個小正方形，如果它們的面積分別是S1、S2，那么S1、S2的大小關系是（ ）組卷：1120引用：69難度：0.7
三．解答題（本題有7題，共60分）
-
26．商場某種新商品每件進價是120元，在試銷期間發現，當每件商品售價為130元時，每天可銷售70件，當每件商品售價高于130元時，每漲價1元，日銷售量就減少1件，據此規律，請回答：
（1）當每件商品售價定為140元時，每天可銷售多少件商品？商場獲得的日盈利是多少？
（2）在上述條件不變，商品銷售正常的情況下，每件商品的銷售價定為多少元，商場日盈利可達1500元？
（3）商家應把商品的單價定為多少元時，可獲得最大利潤，并求出此時的利潤為多少？組卷：137引用：3難度：0.5 -
27．已知，矩形ABCD中，AB=4cm,BC=8cm,AC的垂直平分線EF分別交AD、BC于點E、F，垂足為O．
（1）如圖1，連接AF、CE．求證四邊形AFCE為菱形，并求AF的長；
（2）如圖2，動點P、Q分別從A、C兩點同時出發，沿△AFB和△CDE各邊勻速運動一周．即點P自A→F→B→A停止，點Q自C→D→E→C停止．在運動過程中，
①已知點P的速度為每秒5cm,點Q的速度為每秒4cm,運動時間為t秒，當A、C、P、Q四點為頂點的四邊形是平行四邊形時，求t的值．
②若點P、Q的運動路程分別為a、b（單位：cm,ab≠0），已知A、C、P、Q四點為頂點的四邊形是平行四邊形，求a與b滿足的數量關系式．
組卷：15628引用：94難度：0.3