2022-2023學年海南省文昌中學高二（上）第一次月考數學試卷

一、單選題：本大題共8個小題，每個小題5分，共40分．在每小題給出的選項中，只有一項是符合題目要求的．

• 1．直線

  3

  x-y+1=0的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：1928引用：47難度：0.9

  解析

• 2．已知

  a

  =（λ+1，0，2λ），

  b

  =（6，2μ-1，2），若

  a

  ∥

  b

  ，則λ與μ的值分別為（　　）

  A．-5，-2

  B．5，2

  C． - 1 5 ，- 1 2

  D． 1 5 ， 1 2
  組卷：78引用：21難度：0.9

  解析

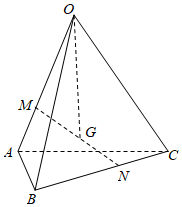• 3．如圖在四面體OABC中，M，N分別在棱OA，BC上且滿足

  OM

  =

  2

  MA

  ，

  BN

  =

  2

  NC

  ，點G是線段MN的中點，用向量

  OA

  ，

  OB

  ，

  OC

  表示向量

  OG

  應為（　　）

  A． OG = 1 3 OA + 1 6 OB + 1 3 OC	B． OG = 1 3 OA + 1 3 OB + 1 6 OC
  C． OG = 1 3 OA + 1 4 OB + 1 4 OC	D． OG = 1 4 OA + 1 4 OB + 1 3 OC
  組卷：509引用：10難度：0.8

  解析

• 4．唐朝詩人李頎的詩《古從軍行》開頭兩句說：“白日登山望烽火，黃昏飲馬傍交河．”詩中隱含著一個有趣的數學問題--“將軍飲馬”問題，即將軍在觀望烽火之后從山腳下某處出發，先到河邊飲馬后再回到軍營，怎樣走才能使總路程最短？在平面直角坐標系中，設軍營所在位置為B（-2，0），若將軍從山腳下的點A（2，0）處出發，河岸線所在直線方程為x+y=3，則“將軍飲馬”的最短總路程為（　　）

  A．4

  B．5

  C． 26

  D．3 2
  組卷：20引用：6難度：0.7

  解析

• 5．經過兩直線l₁：2x-y+3=0與l₂：x+2y-1=0的交點，且平行于直線3x+2y+7=0的直線方程是（　　）

  A．2x-3y+5=0

  B．2x+3y-1=0

  C．3x+2y-2=0

  D．3x+2y+1=0
  組卷：60引用：3難度：0.7

  解析

• 6．1765年，數學家歐拉在其著作《三角形幾何學》中提出：任意三角形的外心、重心、垂心在同一條直線上，這條直線就是后人所說的“歐拉線”．已知△ABC的頂點A（3，0），B（3，5），C（0，1），則△ABC的歐拉線方程為（　　）

  A．3x-y-4=0

  B．x+3y-3=0

  C．x-3y+4=0

  D．3x+y-5=0
  組卷：336引用：2難度：0.6

  解析

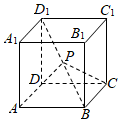• 7．設動點P在棱長為1的正方體ABCD-A₁B₁C₁D₁的對角線BD₁上，

  D

  1

  P

  D

  1

  B

  =λ，當∠APC為銳角時，λ的取值范圍是（　　）

  A．[0， 1 3 ）

  B．[0， 1 2 ）

  C．（ 1 3 ，1）

  D．（ 1 2 ，1）
  組卷：190引用：8難度：0.5

  解析

四、解答題（本小題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．）

• 21．記△ABC的內角A，B，C的對邊分別為a,b,c,分別以a,b,c為邊長的三個正三角形的面積依次為S₁，S₂，S₃．已知S₁-S₂+S₃=

  3

  2

  ，sinB=

  1

  3

  ．
  （1）求△ABC的面積；
  （2）若sinAsinC=

  2

  3

  ，求b.
  組卷：9610引用：18難度：0.4

  解析

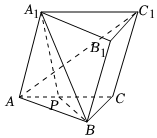• 22．已知三棱柱ABC-A₁B₁C₁中，AC=AA₁=4，BC=2，∠ACB=90°，A₁B⊥AC₁．
  （1）求證：平面A₁ACC₁⊥平面ABC；
  （2）若∠A₁AC=60°，在線段AC上是否存在一點P使平面BA₁P和平面A₁ACC₁所成角的余弦值為

  3

  4

  ？若存在，確定點P的位置；若不存在，說明理由．
  組卷：740引用：16難度：0.6

  解析