當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省泰安二中高一（上）第一次月考數學試卷

發布：2024/4/20 14:35:0

1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，則（?_UA）∪B為（　　）
A．{1，2，4} B．{2，3，4} C．{0，2，3，4} D．{0，2，4}
組卷：1846引用：234難度：0.9
解析
2．命題“對任意x∈R，都有x²-x＞0”的否定為（　　）
A．對任意x∈R，都有x²-x≤0
B．存在x₀∈R，使得x₀²-x₀≤0
C．存在x₀∈R，使得x₀²-x₀＞0
D．不存在x₀∈R，使得x₀²-x₀≤0
組卷：232引用：10難度：0.9
解析
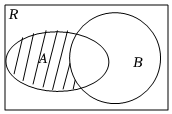3．已知集合A={-2，-1，0，1}，B={x|-1＜x≤1}，則圖中陰影部分所表示的集合為（　　）
A．{-1，0，1} B．{0，1} C．{-2，-1，0} D．{-2，-1}
組卷：553引用：10難度：0.8
解析

4．設甲、乙、丙是三個命題．如果甲是乙的必要條件；丙是乙的充分條件但不是乙的必要條件，那么（　　）

A．丙是甲的充分條件，但不是甲的必要條件

B．丙是甲的必要條件，但不是甲的充分條件

C．丙是甲的充要條件

D．丙不是甲的充分條件，也不是甲的必要條件

組卷：325引用：10難度：0.7

5．設集合A={x|x²-3x-4≤0}，B={x|x²+2x＞0，x∈Z}，則A∩B的真子集共有（　　）
A．15個 B．16個 C．31個 D．32個
組卷：487引用：12難度：0.7
解析
6．已知命題p：x²+2x-3＞0，命題q：x＞a,且q的一個必要不充分條件是p,則實數a的取值范圍是（　　）
A．{a|a≥1} B．{a|a≤1} C．{a|a≥-1} D．{a|a≤-3}
組卷：40引用：1難度：0.9
解析
7．已知集合
M
=
{
x
|
x
=
m
-
5
6
，
m
∈
Z
}
，
N
=
{
x
|
x
=
n
2
-
1
3
，
n
∈
Z
}
，
P
=
{
x
|
x
=
p
2
+
1
6
，
p
∈
Z
}
，則集合M，N，P的關系為（　　）
A．M=N=P B．M?N=P C．M?N∪P D．M?N，N∩P=?
組卷：100引用：1難度：0.6
解析

21．近日，隨著新冠肺炎疫情在多地零星散發，一些城市陸續發出“春節期間非必要不返鄉，就地過年”的倡議．為最大程度減少人員流動，減少疫情發生的可能性，某地政府積極制定政策，決定政企聯動，鼓勵企業在春節期間留住員工在本市過年并加班追產．為此，該地政府決定為當地某A企業春節期間加班追產提供x（0≤x≤20）（萬元）的專項補貼．A企業在收到政府x（萬元）補貼后，產量將增加到t=（x+2）（萬件）．同時A企業生產t（萬件）產品需要投入成本為
（
7
t
+
72
t
+
2
x
）
（萬元），并以每件
（
6
+
40
t
）
元的價格將其生產的產品全部售出．
注：收益=銷售金額+政府專項補貼-成本．
（1）求A企業春節期間加班追產所獲收益R（x）（萬元）關于政府補貼x（萬元）的函數關系式；
（2）當政府的專項補貼為多少萬元時，A企業春節期間加班追產所獲收益最大？
組卷：37引用：1難度：0.5
解析
22．設A={x|x²-（m+3）x+2（m+1）=0，m∈R}，B={x|2x²+（3n+1）x+2=0，n∈R}．
（1）若A∩?_RB=?，求m,n的值；
（2）若對?x∈B，有x∈A，求m,n的取值范圍．
組卷：158引用：1難度：0.5
解析