2021-2022學年上海市普陀區晉元中學高二（上）期末數學試卷

一、填空題（本大題共有12小題，滿分54分）考生應在答題紙相應編號的空格內直接填寫結果，1-6題每個空格填對得4分，7-12題每個空格填對得5分，否則一律得0分.

• 1．若A?面α，B∈面α，C∈面α，則平面ABC與平面α的位置關系為

  ．
  組卷：75引用：2難度：0.7

  解析

• 2．若一個球的體積為

  32

  π

  3

  ，則該球的表面積為

  ．
  組卷：385引用：12難度：0.7

  解析

• 3．在（2x+1）⁵的二項展開式中，各項的系數和為

  .（用數字表示）
  組卷：80引用：2難度：0.8

  解析

• 4．某工廠生產的產品質量進行抽查，數據如下表所示，跟進上表提供的數據，則合格品的概率約為

  .（結果保留兩位小數）
  

  抽查件數	50	100	200	300	500
  合格件數	47	95	192	285	478
  組卷：67引用：2難度：0.9

  解析

• 5．設數列{a_n}的前n項和為S_n，若

  S

  n

  =

  3

  n

  +

  2

  ，則a_n=

  ．
  組卷：634引用：1難度：0.8

  解析

• 6．已知事件A與事件B相互獨立，若

  P

  （

  A

  ∩

  B

  ）

  =

  0

  .

  18

  ，

  P

  （

  A

  ∩

  B

  ）

  =

  0

  .

  12

  ，則P（A）=

  ．
  組卷：228引用：1難度：0.8

  解析

• 7．第14屆國際數學教育大會于7月在上海舉行，大會一共進行8天，設有5位學者分別作個人大會報告，一天只能安排一個報告，且第一天和最后一天不安排報告，則不同的安排方案種數為

  .（用數字作答）
  組卷：121引用：1難度：0.9

  解析

三.解答題（本大題滿分76分）本大題共有5題，解答下列各題必須在答題紙相應編號的規定區域內寫出必要的步驟

• 20．在四棱錐P-ABCD的底面ABCD中，AB∥CD．
  （1）若該四棱錐是正四棱錐，且底面邊長AB=2，PA=4，求四棱錐P-ABCD的表面積；
  （2）如圖1，設PC的中點為F，在側面PBC中能否作出一條直線段使其與AD平行？如果能，請寫出作圖的過程并給出證明；如果不能，請說明理由．
  （3）如圖2，設底面四邊形ABCD是正方形，PD⊥平面ABCD，PD=AD=2，點E，F分別為線段PD和PC的中點，在線段BC上是否存在一點Q，使得點D與平面EFQ的距離恰為

  4

  5

  ？若存在，求出線段BQ的長；若不存在，請說明理由．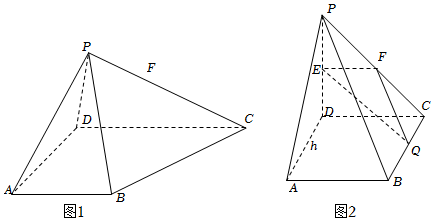
  
  組卷：282引用：1難度：0.5

  解析

• 21．定義：對于任意大于零的自然數n,滿足條件

  a

  n

  +

  a

  n

  +

  2

  2

  ≤

  a

  n

  +

  1

  且a_n≤M（M是與n無關的常數）的無窮數列{a_n}稱為M數列．
  （1）若等差數列{b_n}的前n項和為S_n，且b₁=-3，S₉=-18，判斷數列{b_n}是否是M數列，并說明理由；
  （2）若各項為正數的等比數列{c_n}的前n項和為T_n，且

  c

  2

  =

  1

  2

  ，

  c

  5

  =

  1

  16

  ，證明：數列{T_n}是M數列；
  （3）設數列{d_n}是各項均為正整數的M數列，求證：d_n≤d_n+1．
  組卷：203引用：4難度：0.3

  解析