2017年第十三屆小學“新希望杯”全國數學邀請賽武漢賽區決賽試卷(六年級B卷)
發布:2024/11/2 8:30:2
一、選擇題(每小題4分,共24分)
-
1.若六年級一班的及格率是95%,則不及格人數與總人數的比是( )
A.1:17 B.1:18 C.1:19 D.1:20 組卷:26引用:1難度:0.9 -
2.滬昆高鐵最后一段貴陽至昆明于2016年12月28日開通運營,這對我國“一帶一路”戰略的實施和區域經濟發展都有著重大意義,G1379次高鐵7:42從上海虹橋站出發,當天20:29到達昆明南站,全程共1569千米.途中站點共計停車1小時29分鐘,扣除停車時間,G1379次高鐵的平均速度為( )千米/時.(結果保留整數)
A.137 B.138 C.139 D.140 組卷:36引用:1難度:0.9 -
3.按照如圖所示的規律,圖6中小三角形共有( )個.
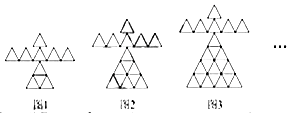
A.51 B.53 C.55 D.57 組卷:42引用:1難度:0.9 -
4.將1千克甲種酒精與2千克濃度為20%的乙種酒精混合后,濃度變為24%,甲種酒精的濃度為( )
A.32% B.34% C.36% D.38% 組卷:230引用:1難度:0.9 -
5.《“楓葉新希望杯”全國數學大賽培訓教程》的正文共199頁,頁碼是從1到199的連續自然數,這本書正文的頁碼共有( )個數碼“1”.
A.139 B.140 C.141 D.142 組卷:138引用:1難度:0.7 -
6.水池有甲、乙兩根出水管,單獨打開甲進水管8小時可將滿水池排空,單獨打開乙出水管6小時可將滿水池排空.如果按甲、乙、甲、…的順序輪流打開1小時,將滿水池排空需( )小時.
A.7 B.6 37C.4 D.3 37組卷:118引用:1難度:0.9
三、解答題(寫出必要的解題過程,共46分)
-
19.從1,2,3,…,90這90個數中任意選取n個數.
(1)若選取的n個數中,必定有兩個數的和是91,求n的最小值;
(2)當n=14時,選取的數中是否一定存在4個數a、b、c、d,使得(a-b)×(c-d)是91的倍數,請說明理由.組卷:30引用:1難度:0.1 -
20.已知n號小正方體的六個面都標有數字n,在圖1的基礎上,將2號小正方體與1號小正方體相鄰堆積,得到圖2
;再將3號小正方體與2號小正方體相鄰堆積,得到圖3;…按這樣的方式堆積成圖5所示的大長方體.
(1)若底面為第1層,那么圖5中第3層12個小正方體的編號(共12個)之和是多少?
(2)在圖5的基礎上拿掉一些小正方體,得到如圖6所示的立體圖形,該立體圖形表面(含底面)上的所有數字之和是多少?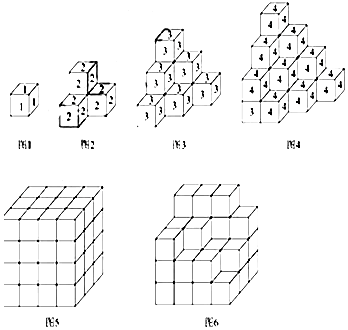 組卷:49引用:3難度:0.5
組卷:49引用:3難度:0.5


