當前位置：試卷中心 > 試卷詳情

2021-2022學年陜西省西安市長安一中高三（下）第五次質檢數學試卷（理科）

發布：2024/12/28 6:30:2

一、選擇題（本題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．已知集合M={m|m=iⁿ，n∈N}，其中i為虛數單位，則下列元素屬于集合M的是（　　）
A．（1-i）（1+i） B．
1
-
i
1
+
i
C．
i
1
-
i
D．（1-i）²
組卷：29引用：3難度：0.7
解析
2．已知函數f（x）=2^x+x,g（x）=log₂x+x,h（x）=x³+x的零點分別為a,b,c,則a,b,c的順序為（　　）
A．a＜b＜c B．a＜c＜b C．c＜b＜a D．c＜a＜b
組卷：175引用：3難度：0.6
解析
3．已知向量
a
=（cosα，-2），
b
=（sinα，1），且
a
∥
b
，則2sinαcosα等于（　　）
A．3 B．-3 C．
-
4
5
D．
4
5
組卷：297引用：6難度：0.7
解析
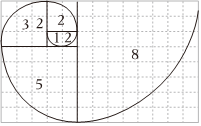4．意大利數學家列昂納多?斐波那契是第一個研究了印度和阿拉伯數學理論的歐洲人，斐波那契數列被譽為是最美的數列，斐波那契數列{a_n}滿足a₁=1，a₂=1，
a
n
=
a
n
-
1
+
a
n
-
2
（
n
≥
3
，
n
∈
N
*
）
．若將數列的每一項按照下圖方法放進格子里，每一小格子的邊長為1，記前n項所占的格子的面積之和為S_n，每段螺旋線與其所在的正方形所圍成的扇形面積為c_n，則其中不正確結論的是（　　）
A．
S
n
+
1
=
a
2
n
+
1
+
a
n
+
1
?
a
n
B．a₁+a₂+a₃+?+a_n=a_n+2-1
C．a₁+a₃+a₄+?+a_2n-1=a_2n-1
D．4（c_n-c_n-1）=πa_n-2?a_n+1
組卷：240引用：1難度：0.3
解析
5．已知正三棱柱ABC-A₁B₁C₁，底面邊長AB=2，AA₁=
3
，則異面直線AB₁與BC所成角的余弦值（　　）
A．
5
6
B．
5
5
C．
7
7
D．
2
2
組卷：110引用：3難度：0.7
解析
6．已知x+y＞0，則“x＞0”是“2^|x|+x²＞2^|y|+y²”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：128引用：5難度：0.7
解析
7．已知ω＞0，|φ|
≤
π
2
，在函數f（x）=sin（ωx+φ），g（x）=cos（ωx+φ）的圖象的交點中，相鄰兩個交點的橫坐標之差的絕對值為
π
2
，當x∈（-
π
6
，
π
4
）時，函數f（x）的圖象恒在x軸的上方，則φ的取值范圍是（　　）
A．（
π
6
，
π
3
） B．[
π
6
，
π
3
] C．（
π
3
，
π
2
） D．[
π
3
，
π
2
]
組卷：2678引用：7難度：0.3
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、[選修4-4：坐標系與參數方程選講]

22．在直角坐標系xOy中，曲線C的參數方程是
x
=
cosφ
y
=
2
sinφ
（φ為參數）以坐標原點為極點，x軸正半軸為極軸建立極坐標系，A，B為曲線C上兩點，且OA⊥OB，設射線OA：
θ
=
α
（
0
＜
α
＜
π
2
）
．
（1）求曲線C的極坐標方程；
（2）求|OA|?|OB|的最小值．
組卷：132引用：4難度：0.6
解析

[選修4-5：不等式選講]

23．已知a,b,c為正數．
（1）證明
2
b
+
c
-
3
a
3
a
+
3
a
+
c
-
2
b
2
b
+
3
a
+
2
b
-
c
c
≥3；
（2）求
a
4
+
b
4
+
c
4
+
（
1
a
+
1
b
+
1
c
）
4
的最小值．
組卷：53引用：5難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．充分不必要條件	B．必要不充分條件
C．充分必要條件	D．既不充分也不必要條件

2021-2022學年陜西省西安市長安一中高三（下）第五次質檢數學試卷（理科）

一、選擇題（本題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．已知集合M={m|m=in，n∈N}，其中i為虛數單位，則下列元素屬于集合M的是（ ）

2．已知函數f（x）=2x+x,g（x）=log2x+x,h（x）=x3+x的零點分別為a,b,c,則a,b,c的順序為（ ）

3．已知向量a=（cosα，-2），b=（sinα，1），且a∥b，則2sinαcosα等于（ ）

5．已知正三棱柱ABC-A1B1C1，底面邊長AB=2，AA1=3，則異面直線AB1與BC所成角的余弦值（ ）

6．已知x+y＞0，則“x＞0”是“2|x|+x2＞2|y|+y2”的（ ）

7．已知ω＞0，|φ|≤π2，在函數f（x）=sin（ωx+φ），g（x）=cos（ωx+φ）的圖象的交點中，相鄰兩個交點的橫坐標之差的絕對值為π2，當x∈（-π6，π4）時，函數f（x）的圖象恒在x軸的上方，則φ的取值范圍是（ ）

四、[選修4-4：坐標系與參數方程選講]

[選修4-5：不等式選講]

23．已知a,b,c為正數．（1）證明2b+c-3a3a+3a+c-2b2b+3a+2b-cc≥3；（2）求a4+b4+c4+（1a+1b+1c）4的最小值．

1．已知集合M={m|m=iⁿ，n∈N}，其中i為虛數單位，則下列元素屬于集合M的是（　　）

2．已知函數f（x）=2^x+x,g（x）=log₂x+x,h（x）=x³+x的零點分別為a,b,c,則a,b,c的順序為（　　）

3．已知向量
a
=（cosα，-2），
b
=（sinα，1），且
a
∥
b
，則2sinαcosα等于（　　）

5．已知正三棱柱ABC-A₁B₁C₁，底面邊長AB=2，AA₁=
3
，則異面直線AB₁與BC所成角的余弦值（　　）

6．已知x+y＞0，則“x＞0”是“2^|x|+x²＞2^|y|+y²”的（　　）

7．已知ω＞0，|φ|
≤
π
2
，在函數f（x）=sin（ωx+φ），g（x）=cos（ωx+φ）的圖象的交點中，相鄰兩個交點的橫坐標之差的絕對值為
π
2
，當x∈（-
π
6
，
π
4
）時，函數f（x）的圖象恒在x軸的上方，則φ的取值范圍是（　　）

23．已知a,b,c為正數．
（1）證明
2
b
+
c
-
3
a
3
a
+
3
a
+
c
-
2
b
2
b
+
3
a
+
2
b
-
c
c
≥3；
（2）求
a
4
+
b
4
+
c
4
+
（
1
a
+
1
b
+
1
c
）
4
的最小值．