2023-2024學年安徽省宣城中學高二（上）第一次月考數學試卷（10月份）

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．在三棱柱ABC-A₁B₁C₁中，可以作為空間向量一組基底的是（　　）

  A． AB ， BC ， A 1 C 1	B． AB ， A B 1 ， A A 1
  C． AB ， AC ， A A 1	D． A A 1 ， AC ， A 1 C 1
  組卷：32引用：2難度：0.5

  解析

• 2．設直線l的斜率為k,且-1≤k＜

  3

  ，求直線l的傾斜角α的取值范圍（　　）

  A． [ 0 ， π 3 ） ∪ （ 3 π 4 ， π ）	B． [ 0 ， π 6 ） ∪ （ 3 π 4 ， π ）
  C． （ π 6 ， 3 π 4 ）	D． [ 0 ， π 3 ） ∪ [ 3 π 4 ， π ）
  組卷：483引用：21難度：0.8

  解析

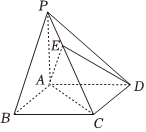• 3．我國古代數學名著《九章算術》中，將底面為矩形且一側棱垂直于底面的四棱錐稱為陽馬．如圖，四棱錐P-ABCD為陽馬，PA⊥平面ABCD，且EC=2PE，若

  DE

  =

  x

  AB

  +

  y

  AC

  +

  z

  AP

  ，則x+y+z=（　　）

  A．1

  B．2

  C． 1 3

  D． 5 3
  組卷：1318引用：34難度：0.7

  解析

• 4．過點A（1，4）的直線在兩坐標軸上的截距之和為零，則該直線方程為（　　）

  A．x-y+3=0	B．x+y-5=0
  C．4x-y=0或x+y-5=0	D．4x-y=0或x-y+3=0
  組卷：1026引用：27難度：0.7

  解析

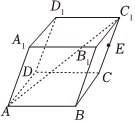• 5．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，以頂點A為端點的三條棱長都是a,且AB⊥AD，∠A₁AB=∠A₁AD=60°，E為CC₁的中點，則點E到直線AC₁的距離為（　　）

  A． 5 10 a

  B． 5 5 a

  C． 5 4 a

  D． 5 3 a
  組卷：166引用：5難度：0.5

  解析

• 6．直線x-2y-1=0關于直線y-x=0對稱的直線方程是（　　）

  A．2x-y+1=0

  B．2x+y-1=0

  C．2x+y+1=0

  D．x+2y+1=0
  組卷：225引用：3難度：0.6

  解析

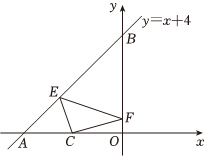• 7．如圖，一次函數y=x+4的圖象與x軸，y軸分別交于點A，B，點C（-2，0）是x軸上一點，點E，F分別為直線y=x+4和y軸上的兩個動點，當△CEF周長最小時，點E，F的坐標分別為（　　）

  A． E （ - 5 2 ， 3 2 ） ，F（0，2）	B．E（-2，2），F（0，2）
  C． E （ - 5 2 ， 3 2 ） ， F （ 0 ， 2 3 ）	D．E（-2，2）， F （ 0 ， 2 3 ）
  組卷：546引用：7難度：0.8

  解析

四、解答題（本大題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．）

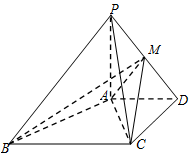• 21．如圖，在四棱錐中P-ABCD，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD=CD=2

  2

  ，BC=4

  2

  ，PA=2．
  （1）求證：AB⊥PC；
  （2）在線段PD上，是否存在一點M，使得二面角M-AC-D的大小為45°，如果存在，求BM與平面MAC所成角的正弦值，如果不存在，請說明理由．
  組卷：621引用：11難度：0.5

  解析

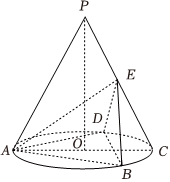• 22．如圖，P為圓錐的頂點，O是圓錐底面的圓心，AC為底面直徑，△ABD為底面圓O的內接正三角形，且△ABD的邊長為

  3

  ，點E在母線PC上，且

  AE

  =

  3

  ，CE=1．
  （1）求證：直線PO∥平面BDE，并求三棱錐P-BDE的體積：
  （2）若點M為線段PO上的動點，當直線DM與平面ABE所成角的正弦值最大時，求此時點M到平面ABE的距離．
  組卷：115引用：5難度：0.5

  解析