2022-2023學年北京師大二附中高二（下）期中數(shù)學試卷

一、選擇題。（共10小題；共40分）

• 1．已知{a_n}為等差數(shù)列，a₅=4，則a₄+a₆=（　　）

  A．4

  B．6

  C．8

  D．10
  組卷：643引用：4難度：0.7

  解析

• 2．函數(shù)f（x）=ax²+bx+c（a≠0）在x=1處的瞬時變化率為（　　）

  A．4a

  B．2a+b

  C．b

  D．4a+b
  組卷：116引用：2難度：0.7

  解析

• 3．已知數(shù)列{a_n}的前n項和

  S

  n

  =

  n

  2

  -

  7

  n

  ，若3＜a_k＜5，則k=（　　）

  A．8

  B．7

  C．6

  D．5
  組卷：485引用：6難度：0.7

  解析

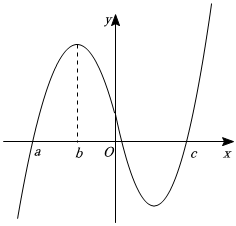• 4．已知函數(shù)y=f′（x）的圖象如圖所示，那么下列結(jié)論正確的是（　　）

  A．f（a）=0	B．f′（x）沒有極大值
  C．x=b時，f（x）有極大值	D．x=c時，f（x）有極小值
  組卷：217引用：3難度：0.5

  解析

• 5．在等比數(shù)列{a_n}中，a₁＞0，則“a₁＜a₄”是“a₃＜a₅”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：259引用：15難度：0.9

  解析

• 6．與正整數(shù)n有關(guān)的數(shù)學命題，如果當n=k（k∈N，k≥1）時該命題成立，則可推得當n=k+1時該命題成立．現(xiàn)得知n=11時命題不成立，那么可推得（　　）

  A．當n=10時，該命題不成立

  B．當n=12時，該命題不成立

  C．當n=10時，該命題成立

  D．當n=12時，該命題成立
  組卷：90引用：1難度：0.8

  解析

• 7．世界上最早在理論上計算出“十二平均律”的是我國明代杰出的律學家朱載堉，他當時稱這種律制為“新法密率”十二平均律將一個純八度音程分成十二份，依次得到十三個單音，從第二個單音起，每一個單音的頻率與它前一個單音的頻率的比都相等，且最后一個單音是第一個單音頻率的2倍．已知第十個單音的頻率f₁₀=440Hz,則與第四個單音的頻率f₄最接近的是（　　）

  A．880Hz

  B．622Hz

  C．311Hz

  D．220Hz
  組卷：206引用：4難度：0.7

  解析

三、解答題。（共6小題；共85分）

• 20．已知函數(shù)f（x）=e^x-1-msinx（m∈R）．
  （Ⅰ）當m=1時．
  （ⅰ）求曲線y=f（x）在點（0，f（0））處的切線方程；
  （ⅱ）求證：

  ?

  x

  ∈

  （

  0

  ，

  π

  2

  ）

  ，f（x）＞0．
  （Ⅱ）若f（x）在

  （

  0

  ，

  π

  2

  ）

  上恰有一個極值點，求m的取值范圍．
  組卷：852引用：5難度：0.6

  解析

• 21．記項數(shù)為2022且每一項均為正整數(shù)的有窮數(shù)列{a_n}所構(gòu)成的集合為A．若對于任意的p、q∈[1，2022]（p,q∈N），當p+q∈A時，都有a_p+a_q∈A，則稱集合A為“子列封閉集合”．
  （1）若a_n=n（1≤n≤2022，n∈N），判斷集合A是否為“子列封閉集合”，說明理由；
  （2）若數(shù)列{a_n}的最大項為a₂₀₂₂，且A∩[2023，4044]≠?，證明：集合A不是“子列封閉集合”；
  （3）若數(shù)列{a_n}為嚴格遞增數(shù)列，a₂₀₂₂=4046，且集合A為“子列封閉集合”，求數(shù)列{a_n}的通項公式．
  組卷：149引用：4難度：0.1

  解析