2009-2010學年四川省成都七中高二（上）數學單元測試：立體幾何（2）

一、選擇題（共6小題，每小題3分，滿分18分）

• 1．在三棱柱ABC-A₁B₁C₁中，各棱長相等，側棱垂直于底面，點D是側面BB₁C₁C的中心，則AD與平面BB₁C₁C所成角的大小是（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：855引用：65難度：0.9

  解析

• 2．若正四棱柱ABCD-A₁B₁C₁D₁的底面邊長為1，AB₁與底面ABCD成60°角，則A₁C₁到底面ABCD的距離為（　　）

  A． 3 3

  B．1

  C． 2

  D． 3
  組卷：976引用：18難度：0.9

  解析

• 3．已知α，β表示兩個不同的平面，m為平面α內的一條直線，則“α⊥β”是“m⊥β”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：891引用：100難度：0.9

  解析

二、填空題（共4小題，每小題3分，滿分12分）

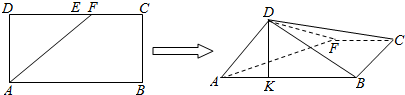
• 10．如圖，在長方形ABCD中，AB=2，BC=1，E為DC的中點，F為線段EC（端點除外）上一動點，現將△AFD沿AF折起，使平面ABD⊥平面ABC，在平面ABD內過點D作DK⊥AB，K為垂足，設AK=t,則t的取值范圍是

  ．
  
  組卷：2013引用：23難度：0.7

  解析

三、解答題（共1小題，滿分0分）

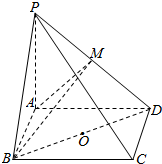• 11．如圖，在四棱錐P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2，以BD的中點O為球心、BD為直徑的球面交PD于點M，
  （1）求證：平面ABM⊥平面PCD；
  （2）求直線PC與平面ABM所成的角；
  （3）求點O到平面ABM的距離．
  組卷：824引用：7難度：0.1

  解析