2022-2023學年四川省遂寧二中高三（上）第五次月考數學試卷（文科）

一、選擇題（本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設m,n是兩條不同的直線，α，β是兩個不同的平面，下列命題中正確的是（　　）

  A．若α⊥β，m?α，n?β，則m⊥n	B．若m⊥α，m∥n,n∥β，則α⊥β
  C．若m⊥n,m?α，n?β，則α⊥β	D．若α∥β，m?α，n?β，則m∥n
  組卷：1512引用：163難度：0.9

  解析

• 2．某圓錐體積為1，用一個平行于圓錐底面的平面截該圓錐得到一個圓臺，若圓臺上底面和下底面半徑之比為

  1

  2

  ，則該圓臺體積為（　　）

  A． 7 8

  B． 3 4

  C． 1 2

  D． 2 2
  組卷：272引用：11難度：0.6

  解析

• 3．已知數列{a_n}的前n項和為

  S

  n

  ，

  a

  n

  +

  1

  =

  S

  n

  +

  2

  n

  +

  1

  ，

  a

  1

  =

  2

  ，則S_n=（　　）

  A．（n+1）?2n

  B．（n+1）?2n-1

  C．n?2n-1

  D．n?2n
  組卷：229引用：3難度：0.5

  解析

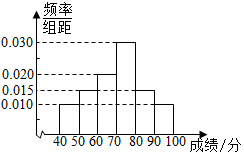• 4．在某次高中學科競賽中，4000名考生的參賽成績統計如圖所示，60分以下視為不及格，若同一組中數據用該組區間中點作代表，則下列說法中有誤的是（　　）

  A．成績在[70，80]分的考生人數最多

  B．考生競賽成績的中位數為75分

  C．不及格的考生人數為1000人

  D．考生競賽成績的平均分約70.5分
  組卷：122引用：4難度：0.7

  解析

• 5．函數

  y

  =

  （

  1

  +

  cosx

  ）

  （

  x

  -

  1

  x

  ）

  的部分圖象大致為（　　）

  A．

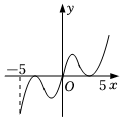
  B．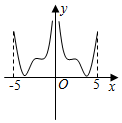

  C．

  D．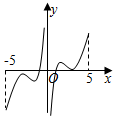
  組卷：544引用：6難度：0.5

  解析

• 6．已知奇函數f（x）在R上是增函數，g（x）=xf（x）．若a=g（-log₂5.1），b=g（2^0.5），c=g（3），則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．c＜b＜a

  D．b＜c＜a
  組卷：310引用：6難度：0.6

  解析

• 7．若函數f（x）=lnx+ax²-2在區間

  （

  1

  2

  ，

  2

  ）

  內存在單調遞增區間，則實數a的取值范圍是（　　）

  A．（-∞，-2]

  B．（-2，+∞）

  C．（-2，- 1 8 ）

  D． [ - 1 8 ， + ∞ ）
  組卷：571引用：18難度：0.7

  解析

選做題（多做，按照第一題計分）

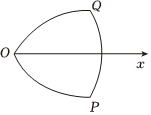• 22．以等邊三角形的每個頂點為圓心，以其邊長為半徑，在另兩個頂點間作一段圓弧，三段圓弧圍成的曲邊三角形被稱為勒洛三角形．如圖，在極坐標系Ox中，曲邊三角形OPQ為勒洛三角形，且

  P

  （

  2

  ，-

  π

  6

  ）

  ，

  Q

  （

  2

  ，

  π

  6

  ）

  ．以極點O為極坐標原點，極軸Ox為x軸正半軸建立平面直角坐標系xOy.
  （1）求

  ?

  OQ

  的極坐標方程；
  （2）若曲線C的參數方程為

  x = - 1 2 t

  y = 2 + 3 2 t

  （t為參數），求曲線C與

  ?

  OQ

  交點的極坐標．
  組卷：98引用：7難度：0.6

  解析

[選修4-5：不等式選講]（本題滿分0分）

• 23．已知函數f（x）=|x+1|+|x+2|的最小值為m.
  （1）求m；
  （2）已知a,b,c為正數，且abc=4m,求（a+b）²+c²的最小值．
  組卷：14引用：5難度：0.6

  解析