2022-2023學年江蘇省常州市金壇區高二（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知隨機變量X～N（5，1），且P（4＜x＜6）=m,P（3＜x＜7）=n,則P（3＜x＜6）的值為（　　）

  A． m + n 2

  B． n - m 2

  C． 1 - m 2

  D． 1 - n 2
  組卷：223引用：1難度：0.8

  解析

• 2．已知兩條異面直線a,b上分別有4個點和7個點，則這11個點可以確定不同的平面個數為（　　）

  A．4

  B．7

  C．11

  D．126
  組卷：68引用：1難度：0.8

  解析

• 3．若（1+mx）（1-x）⁵的展開式中不含x³項，則實數m的值為（　　）

  A．-2

  B．-1

  C．0

  D．1
  組卷：178引用：1難度：0.9

  解析

• 4．在4次獨立試驗中，事件A出現的概率相同，若事件A至少發生一次的概率是

  80

  81

  ，則事件A在一次試驗中出現的概率為（　　）

  A． 1 3

  B． 1 2

  C． 2 3

  D． 3 4
  組卷：73引用：1難度：0.7

  解析

• 5．將邊長為a的正三角形ABC沿BC邊上的高線AD折成120°的二面角，則點A到BC邊的距離是（　　）

  A． 13 4 a

  B． 3 2 a

  C． 2 2 a

  D． 3 3 a
  組卷：122引用：1難度：0.5

  解析

• 6．某考生回答一道四選一的單項選擇考題，假設他知道正確答案的概率為0.6，知道正確答案時，答對的概率為100%，而不知道正確答案時，猜對的概率為0.2，那么他答對題目的概率為（　　）

  A．0.8

  B．0.68

  C．0.6

  D．0.2
  組卷：526引用：3難度：0.8

  解析

• 7．學校環保節活動期間，某班有甲、乙、丙、丁四名學生參加了志愿者工作．將這四名學生分配到A，B，C三個不同的環保崗位，每個崗位至少分配一名學生，若甲要求不分配到B崗位，則不同的分配方案的種數為（　　）

  A．30

  B．24

  C．20

  D．18
  組卷：108引用：1難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．某校為了普及科普知識，增強學生的科學素養，在全校組織了一次科普知識競賽．經過初賽、復賽，甲、乙兩個代表隊（每隊3人）進入了決賽．規定每人回答一個問題，答對者為本隊贏得10分，答錯者得0分．假設甲隊中3人答對的概率分別為

  4

  5

  ，

  3

  4

  ，

  2

  3

  ，乙隊中每人答對的概率均為

  3

  4

  ，且各人回答正確與否相互之間沒有影響，用ξ表示甲隊的總得分．
  （1）求ξ的分布列和數學期望；
  （2）求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率．
  組卷：110引用：1難度：0.6

  解析

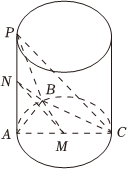• 22．如圖，三角形ABC是圓柱底面圓的內接三角形，PA為圓柱的母線，M，N分別是AC和PA的中點，平面PBC⊥平面PAB，PA=AB=BC=2．
  （1）求證：BC⊥AB；
  （2）求三棱錐N-ABM和圓柱的體積之比；
  （3）求平面PBC與平面MBN所成的銳二面角的大小．
  組卷：29引用：1難度：0.5

  解析