2023-2024學年上海市楊浦高級中學高二（上）期中數學試卷

一、填空題（本大題共有12小題，滿分54分，第1～6題每題4分，第7～12題每題5分）考生應在答題紙相應位置填寫結果．

• 1．用集合符號表述語句“平面α經過直線l”：

  ．
  組卷：89引用：5難度：0.8

  解析

• 2．橢圓

  x

  2

  2

  +

  y

  2

  6

  =

  1

  的焦點坐標為

  ．
  組卷：37引用：4難度：0.7

  解析

• 3．雙曲線

  x

  2

  4

  -

  y

  2

  =

  1

  的兩條漸近線的直線方程是

  ．
  組卷：58引用：1難度：0.9

  解析

• 4．過圓x²+y²=5上一點M（1，2）的圓的切線方程為

   

  ．
  組卷：35引用：6難度：0.5

  解析

• 5．已知空間中兩個角α，β，且角α與角β的兩邊分別平行，若α=70°，則β=

  ．
  組卷：15引用：5難度：0.7

  解析

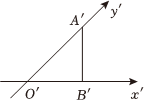• 6．如圖是水平放置的△AOB的斜二測直觀圖，其中O′B′=2，∠A′B′O′=90°，則在△AOB中，AB=

  ．
  組卷：40引用：4難度：0.7

  解析

• 7．已知△ABC所在平面外一點P，且PA，PB，PC兩兩垂直，則點P在平面ABC內的射影應為△ABC的

  心．
  組卷：222引用：2難度：0.6

  解析

三、解答題（本大題共有5題，滿分78分）解答下列各題必須在答題紙相應編號的規定區域內寫出必要的步驟．

• 20．已知以F（1，0）為焦點的拋物線C₁的頂點為原點，點P是拋物線C₁的準線上任意一點，過點P作拋物線C₁的兩條切線PA、PB，其中A、B為切點，設直線PA、PB的斜率分別為k₁、k₂．
  （1）求拋物線C₁的標準方程；
  （2）若點P的縱坐標為1，計算k₁?k₂的值；
  （3）求證：直線AB過定點，并求出這個定點的坐標．
  組卷：132引用：1難度：0.6

  解析

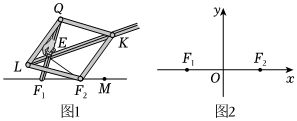• 21．17世紀荷蘭數學家舒騰設計了多種圓錐曲線規，其中的一種如圖1所示．四根等長的桿用鉸鏈首尾鏈接，構成菱形LF₂KQ．帶槽桿QF₁長為

  2

  2

  ，點F₁，F₂間的距離為2，轉動桿QF₁一周的過程中始終有|QE|=|EF₂|．點M在線段F₁F₂的延長線上，且|MF₂|=1．
  （1）建立如圖2所示的平面直角坐標系，求出點E的軌跡Γ的方程；
  （2）過點F₂的直線l₁與Γ交于A，B兩點．記直線MA，MB的斜率為k₁，k₂，證明：k₁+k₂為定值；
  （3）過點M作直線l₂垂直于直線F₁F₂，在l₂上任取一點N，對于（2）中的A，B兩點，試證明：直線NA，NF₂，NB的斜率成等差數列．
  組卷：218引用：3難度：0.1

  解析