當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年新疆喀什地區(qū)巴楚縣高二（上）期中數(shù)學(xué)試卷

發(fā)布：2024/10/1 5:0:1

1．對(duì)于空間向量
a
=（1，2，3），
b
=（λ，4，6）．若
a
∥
b
，則實(shí)數(shù)λ=（　　）
A．-2 B．-1 C．1 D．2
組卷：146引用：7難度：0.9
解析
2．在三棱柱ABC-A₁B₁C₁中，若
AB
=
a
，
AC
=
b
，
A
A
1
=
c
，則
C
1
B
=（　　）
A．
a
+
b
-
c
B．
-
a
-
b
+
c
C．
-
a
+
b
-
c
D．
a
-
b
-
c
組卷：114引用：6難度：0.8
解析
3．過兩點(diǎn)（-3，2）和（2，-1）的直線的斜率為（　　）
A．
6
5
B．
3
5
C．
-
6
5
D．
-
3
5
組卷：150引用：9難度：0.8
解析
4．與向量
m
=（4，0，3）同向的單位向量為（　　）
A．（
4
5
，0，
3
5
） B．（
3
5
，0，
4
5
） C．（
2
2
，0，
2
2
） D．（2，0，
3
2
）
組卷：60引用：5難度：0.9
解析
5．直線y=x與直線y=-x+2的交點(diǎn)坐標(biāo)為（　　）
A．（-1，-1） B．（1，1） C．（-1，1） D．（1，-1）
組卷：158引用：4難度：0.8
解析
6．已知直線l₁：mx-y+6=0，l₂：2x+y+3=0，若l₁⊥l₂，則m的值為（　　）
A．-2 B．
-
1
2
C．
1
2
D．2
組卷：123引用：12難度：0.5
解析
7．經(jīng)過點(diǎn)A（3，2），且與直線4x+y-2=0平行的直線方程為（　　）
A．4x+y+2=0 B．4x+y-14=0 C．x-4y-12=0 D．x-4y-14=0
組卷：119引用：12難度：0.9
解析

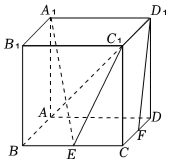21．如圖，在棱長為2的正方體ABCD-A₁B₁C₁D₁中，E，F(xiàn)分別為棱BC，CD的中點(diǎn)．
（1）求證：D₁F∥平面A₁EC₁；
（2）求直線AC₁與平面A₁EC₁所成角的正弦值．
組卷：118引用：21難度：0.6
解析
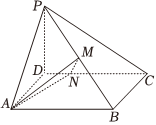22．如圖，四棱錐P-ABCD中，PD⊥平面ABCD，底面四邊形ABCD為矩形，AB=4，BC=2，
PD
=
2
3
，M為PB中點(diǎn)，N為CD靠近D的四等分點(diǎn)．
（1）求證：PB⊥平面AMN；
（2）求二面角M-AN-B的余弦值；
（3）求點(diǎn)D到平面AMN的距離．
組卷：135引用：5難度：0.5
解析