2022-2023學(xué)年河南省南陽(yáng)市桐柏第一高級(jí)中學(xué)高一（下）期末數(shù)學(xué)試卷

一、選擇題（共8小題，每小題5分，共40分）

• 1．復(fù)數(shù)z=1-i（i為虛數(shù)單位），則

  z

  對(duì)應(yīng)復(fù)平面內(nèi)的點(diǎn)位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：10引用：2難度：0.7

  解析

• 2．“有兩個(gè)面平行，其余各面都是平行四邊形”是“幾何體為棱柱”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要
  組卷：66引用：4難度：0.7

  解析

• 3．定義向量

  a

  ，

  b

  運(yùn)算

  a

  ×

  b

  結(jié)果是一個(gè)向量，它的模是

  |

  a

  ×

  b

  |

  =

  |

  a

  |

  |

  b

  |

  sin

  ?

  a

  ，

  b

  ?

  ，其中

  ?

  a

  ，

  b

  ?

  表示向量

  a

  ，

  b

  的夾角．已知向量

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，且

  ?

  a

  ，

  b

  ?

  =

  5

  π

  6

  ，則

  |

  a

  ×

  b

  |

  =（　　）

  A．1

  B．-1

  C． 3

  D． - 3
  組卷：17引用：1難度：0.5

  解析

• 4．已知α為銳角，

  sin

  （

  π

  4

  -

  α

  ）

  =

  -

  3

  5

  ，則sinα=（　　）

  A． 2 10

  B． 2 2 5

  C． 3 2 5

  D． 7 2 10
  組卷：243引用：3難度：0.7

  解析

• 5．要得到函數(shù)y=2cos2x的圖象．只需將函數(shù)

  y

  =

  2

  sin

  （

  2

  x

  +

  π

  6

  ）

  的圖象（　　）

  A．向右平移 π 3 個(gè)單位長(zhǎng)度	B．向左平移 π 3 個(gè)單位長(zhǎng)度
  C．向右平移 π 6 個(gè)單位長(zhǎng)度	D．向左平移 π 6 個(gè)單位長(zhǎng)度
  組卷：55引用：2難度：0.7

  解析

• 6．設(shè)m,n為兩條直線，α，β為兩個(gè)平面，下列四個(gè)命題中，正確的命題是（　　）

  A．若m⊥α，n⊥β，α⊥β，則m⊥n

  B．若m∥α，m∥β，n∥α，n∥β，則α∥β

  C．若m⊥n,α∥β，m∥α，則n⊥β

  D．若m∥α，α⊥β，n?β，則m⊥n
  組卷：71引用：2難度：0.6

  解析

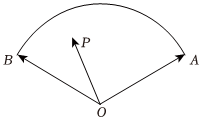• 7．如圖扇形AOB所在圓的圓心角大小為

  2

  π

  3

  ，P是弧AB上任意一點(diǎn)，若

  OP

  =

  x

  OA

  +

  y

  OB

  ，那么2x+y的最小值是（　　）

  A．0

  B． 2 21 3

  C．1

  D． 3 3 2
  組卷：145引用：2難度：0.5

  解析

四、解答題（共6小題，共70分）

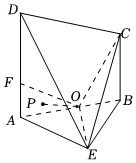• 21．如圖，DA和CB都垂直于平面ABE，F(xiàn)是DA上一點(diǎn)，且CB=4，AF=2，△ABE為等腰直角三角形，且O是斜邊AB的中點(diǎn)，CE與平面ABE所成的角為45°．
  （1）證明：FO⊥平面OCE；
  （2）求二面角F-EC-O的平面角的正切值；
  （3）若點(diǎn)P是平面ADE內(nèi)一點(diǎn)，且OC⊥OP，設(shè)點(diǎn)P到平面ABE的距離為d₁，PA=d₂，求d₁+d₂的最小值．
  組卷：972引用：7難度：0.1

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  sin

  （

  1

  2

  ωx

  ）

  cos

  （

  1

  2

  ωx

  +

  φ

  ）

  ，ω＞0，

  |

  φ

  |

  ≤

  π

  2

  ．
  （1）當(dāng)ω=2，

  φ

  =

  π

  3

  時(shí)，
  ①求f（x）的單調(diào)遞增區(qū)間；
  ②當(dāng)

  x

  ∈

  [

  0

  ，

  π

  2

  ]

  時(shí)，關(guān)于x的方程10[f（x）]²-（10m+1）f（x）+m=0恰有4個(gè)不同的實(shí)數(shù)根，求m的取值范圍．
  （2）函數(shù)g（x）=f（x）+sinφ，

  x

  =

  -

  π

  4

  是g（x）的零點(diǎn)，直線

  x

  =

  π

  4

  是g（x）圖象的對(duì)稱軸，且g（x）在

  （

  π

  18

  ，

  5

  π

  36

  ）

  上單調(diào)，求ω的最大值．
  組卷：228引用：4難度：0.5

  解析